Distancia entre dos puntos

Objetivo

Esta lección presenta los conceptos y destrezas básicas que te permitirán hallar la distancia entre dos puntos en el plano xy.

Introducción: Teorema de Pitágoras

En la siguiente figura se muestra un triángulo rectángulo, con hipotenusa h y catetos c1 y c2

El teorema de Pitágoras indica que

h 2 = c 1 2 + c 2 2


Presione el botón siguiente para practicar usar el teorema de Pitágoras para conseguir lados desconocidos en triangulos rectangulos:


Metodo General para Encontrar la Distancia entre Dos Puntos

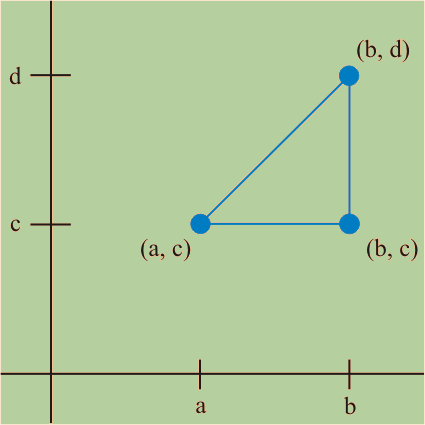
El diagrama siguiente muestre dos puntos (a,c) y (b,d) en un sistema de coordenadas cartesianas,



Para obtener la distancia entre estos dos puntos podemos seguir los siguientes pasos:

Paso1.
Dibujar un triángulo rectángulo con coordenadas (a, c), (b, c) y (b, d)




Paso 2.
Encontrar las longitudes de los catetos del triángulo.



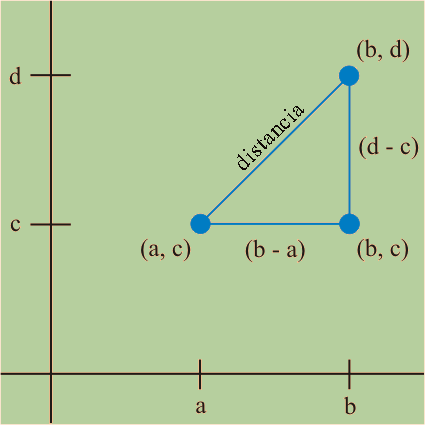
Paso 3.
Calcular la distancia utilizando la fórmula de Pitágoras.

distancia = ( b − a ) 2 + ( d − c ) 2




Ejemplos

Ejemplo 1: Encuentre la distancia entre los puntos (1, 2) y (3, 5).



Solución:

Paso 1 - Dibujar el triangulo rectangulo con vertices (1,2), (3,2) y (3,5).





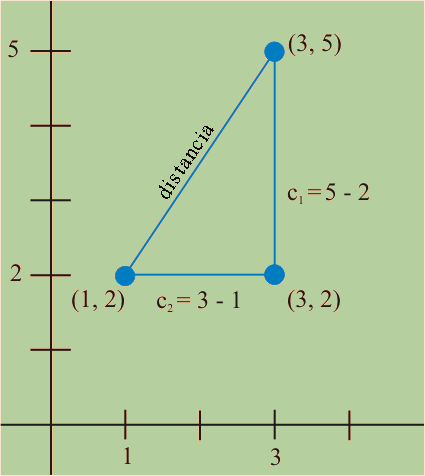
Paso 2 - Encontrar las longitudes de los catetos del triángulo: Ver Diagrama arriba.

Paso 3 - Usar el teorema de Pitagoras para calcular la distancia:

c 1 = 3
c 2 = 2
distancia = ( 3 ) 2 + ( 2 ) 2 = 13

Ejemplo 2: Encuentre la distancia entre los puntos (-1, 2) y (3, -2).

Solución:
Paso 1 - Dibujar el triangulo rectangulo con vertices (-1,2), (3,2) y (3,-2).





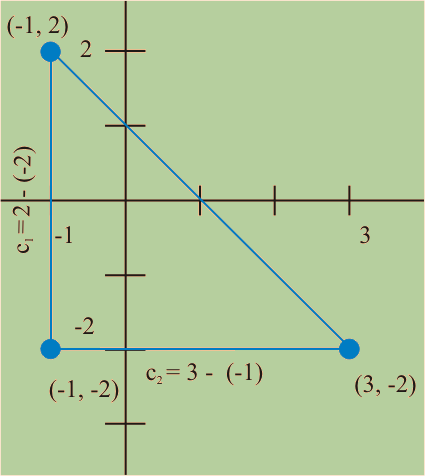
Paso 2 - Encontrar las longitudes de los catetos del triángulo: Ver Diagrama arriba.

Paso 3 - Usar el teorema de Pitagoras para calcular la distancia:

c 1 = 2
c 2 = 3
distancia = ( 4 ) 2 + ( 4 ) 2 = 32


Crear tus Propios Ejemplos

Esta actividad te permite crear tus propios ejemplos. Cuando das 'clik' en dos puntos, el cambio en x se muestra en el color amarillo, el cambio en y se muestra en el color verde y la distancia entre los dos puntos se muestra en rojo. Finalmente, esos datos se usan para calcular la distancia entre los puntos.



Presione el enlace de abajo para practicar ejercicios de distancia entre dos puntos:


Resumen

Al terminar esta lección, debes entender los conceptos y destrezas básicas para hallar la distancia entre dos puntos en el plano xy.