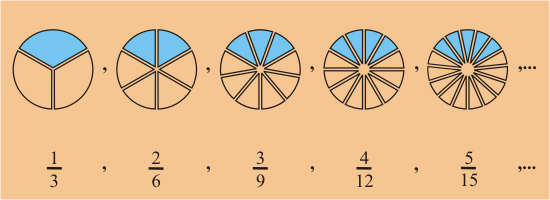Fracciones
Objetivos
Esta lección presenta los conceptos y destrezas básicas que te permitirán:
- Encontrar la fracción que muestra una parte de un todo en un diagrama.
- Encontrar en un diagrama a que parte del todo corresponde una fracción dada.
- Identificar y encontrar fracciones equivalentes a una fracción dada.
- Expresar una fracción en su forma más simple.
- Convertir números mixtos en fracciones impropias y vice versa.
Introducción
Para saber el número de canicas o monedas que tenemos en un frasco, lo único que necesitamos son los números naturales (1,2,3,...). Sin embargo, si queremos medir la cantidad de bizcocho que nos sirvieron después de la cena, el caso no es el mismo. Seguramente que nos sirvieron un pedazo o una porción del bizcocho y no uno, ni dos bizcochos. En este caso tenemos que considerar un nuevo conjunto de números que puede representar partes de un todo. Las fracciones son tales números.
Definición
Una fracción suele representarse como dos números
organizados verticalmente con una línea entre ellos. El número sobre la línea es
llamado el numerador y el número bajo la línea es llamado el denominador.
Significado del Denominador
El denominador de una fracción se refiere al número de partes iguales en las que se ha dividido un todo.
Ejemplos:
1) Por ejemplo, si tenemos una pizza y la dividimos en dos partes, nuestra fracción asociada tendrá como denominador el número 2.

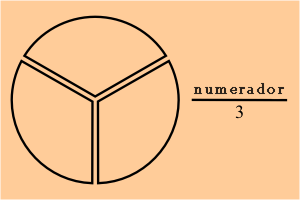
2) Si dividimos nuestra pizza en tres partes, nuestra fracción asociada tendrá como denominador el número 3.
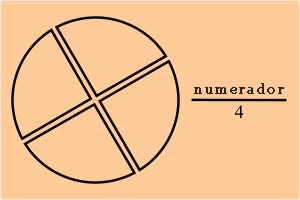
3) Si dividimos nuestra pizza en cuatro partes, nuestra fracción asociada tendrá como denominador el número 4.
Significado del Numerador
Hemos aprendido que el denominador de una fracción se refiere al número de partes iguales en las que se ha dividido una cantidad completa. El numerador de una fracción se refiere al número de estas partes que nosotros tomamos.
Ejemplos:
1) Si dividimos una pizza en cuatro partes, nuestra fracción asociada tendrá 4 en el denominador para indicar que hemos dividido la pizza en cuatro partes. Si tomamos tres de esas partes, la fracción tendrá como numerador el número 3.
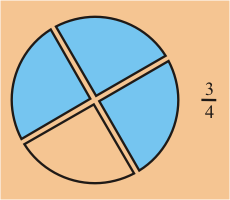
2) Si dividimos una pizza en tres partes, nuestra fracción asociada tendrá 3 en el denominador para indicar que la hemos dividido en tres partes. Si tomamos dos (2) de esas partes, el numerador será entonces 2.
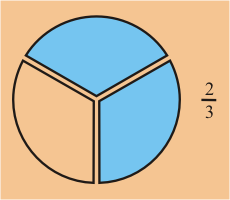
Presione el botón de abajo para practicar en forma visual la relación entre numerador, denominador y la fracción asociada.

Presione el botón de abajo para practicar en forma visual a identificar la fracción correcta de un todo.

Fracciones equivalentes
Hasta aquí hemos aprendido a utilizar el numerador y el denominador para obtener las partes de un todo asociadas con una fracción.
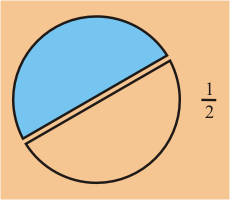 |
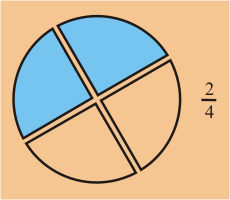 |
En el diagrama es claro que todas las fracciones se refieren a la misma cantidad.
Fíjate bien.
Ejemplo 2:
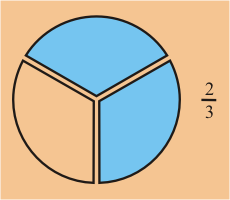
|

|
En los ejemplos anteriores hemos visto que ,
, se refieren a la misma cantidad y es por eso que se le llaman
fracciones equivalentes. Las Fracciones Equivalentes tienen el mismo valor, aunque parezcan diferentes.
Los enteros se pueden representar como fracciones. Por ejemplo 2 es lo mismo que . Es bueno que recuerdes que la raya entre el numerador y el denominador es realmente el operador de división. Vea la representación del entero 2 en el diagrama de abajo.
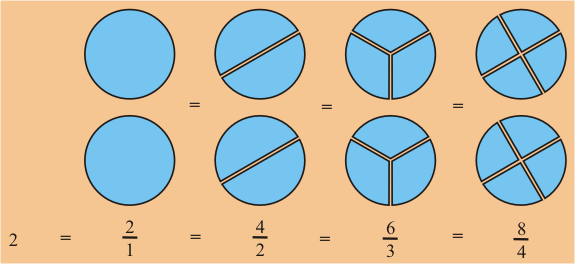
Presione en el botón para practicar realizando conversiones entre números mixtos y fracciones impropias:

Fracciones en su forma más simple
Hemos visto que hay muchas maneras de expresar la misma cantidad utilizando fracciones. Teniendo en cuenta todas las representaciones posibles de una cantidad, si seleccionamos la fracción donde el numerador y denominador tienen los valores más pequeños posibles, se dice que la fracción está su forma más simple.
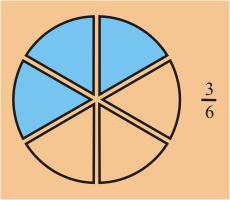
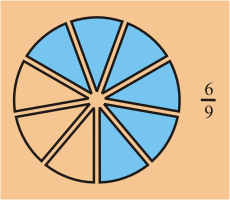
Ejemplo: La fracción representada en la primera figura tiene fracciones equivalentes que se muestran en la segunda figura.
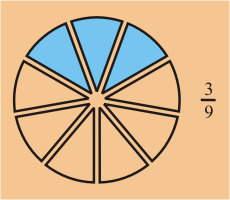
Por lo tanto, en su forma más simple sería .
Práctica:
Presione en el botón para practicar realizando ejercicios de simplificación de fracciones:

Números Mixtos y Fracciones Impropias
Las fracciones impropias y los números mixtos son usados en casos en que tenemos uno o más enteros y una fracción. Consideremos el caso en que tenemos 3 y
bizcochos.
¿Cómo se puede interpretar esto?

La expresión consistente con esta interpretación es llamada número mixto, el cual consiste en un número entero seguido por una fracción.
En este caso, un número mixto para representar tres y dos tercios bizcochos es
.
2. La segunda forma de interpretar esto es como 11 pedazos de bizcocho, donde cada pedazo es de un bizcocho completo.
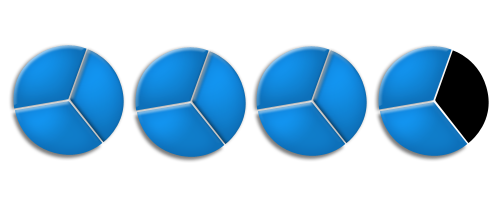
La expresión consistente con esta interpretación es llamada fracción impropia. Usando la definición del numerador y del denominador dadas anteriormente, podemos rápidamente encontrar que es la fracción impropia apropiada para representar 3 y dos tercios bizcochos.
La siguiente tabla presenta otros ejemplos de números mixtos con la respectiva fracción impropia asociada.
| Número mixto | ||||
| Fracción impropia asociada |
Presione en el botón para practicar realizando conversiones entre números mixtos y fracciones impropias:

Resumen
Ahora que terminaste la lección, deberías ser capaz de hacer lo siguiente:
- Encontrar la fracción que muestra una parte de un todo en un diagrama.
- Encontrar en un diagrama a que parte del todo corresponde una fracción dada.
- Identificar y encontrar fracciones equivalentes a una fracción dada.
- Expresar una fracción en su forma más simple.
- Convertir números mixtos en fracciones impropias y vice versa.