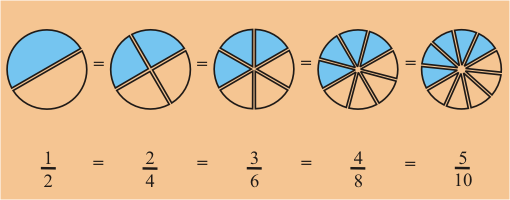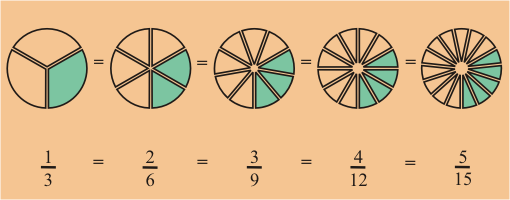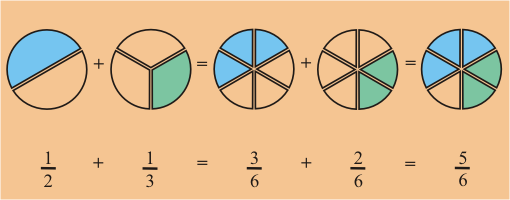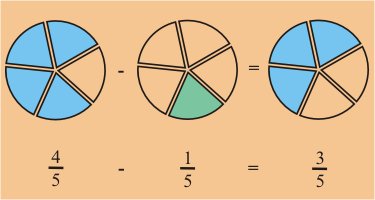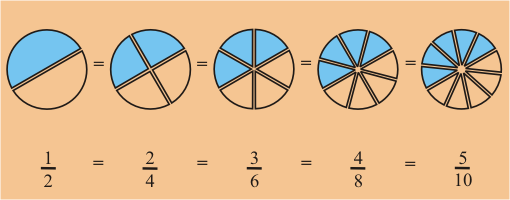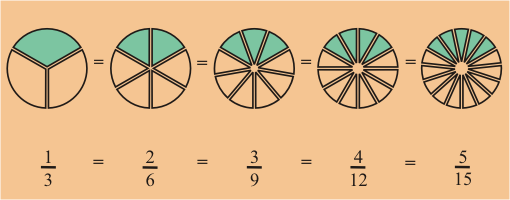Objetivos
Esta lección presenta procesos básicos de fracciones que le permitirán hacer lo siguiente:
- Hallar el mínimo común denominador de dos fracciones.
- Sumar y restar fracciones.
- Multiplicar y dividir fracciones
Suma de fracciones
El sumar fracciones con el mismo denominador resulta sencillo. A estas fracciones se les conoce como fracciones homogéneas.
Ejemplo 1:
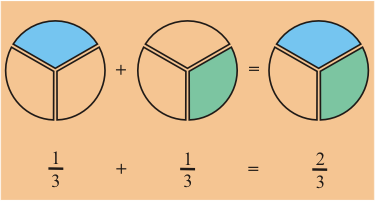
Ejemplo 2:
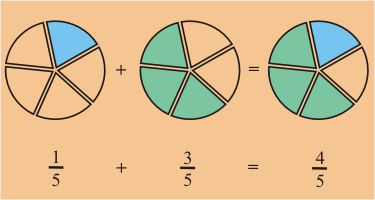
La operación de suma cuando tenemos fracciones homogéneas, consiste simplemente en sumar los numeradores (partes del todo) manteniendo igual las partes que corresponden al todo o sea el denominador.
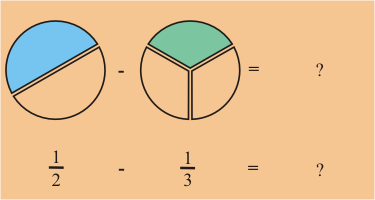
Sin embargo, si las fracciones son heterogéneas, o sea tienen distintos denominadores el proceso no es tan simple.
Ejemplo:
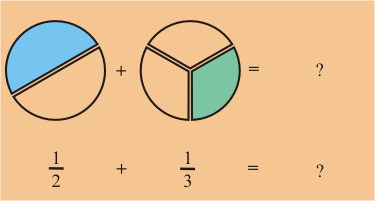
Podemos visualizar la cantidad que
refleja esta suma facilmente. Sin embargo, expresar dicha suma es más dificil.
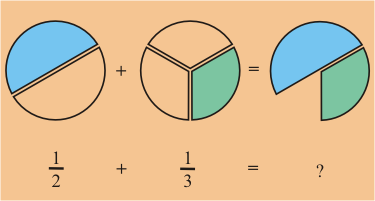
Si recordamos que las fracciones pueden ser expresadas en múltiples formas, podremos solucionar este problema.
Un método para hallar la solución de :
-
Encuentre fracciones equivalentes
usando los denominadores posibles
-
Seleccione el denominador común más pequeño
a ambas expansiones y exprese las fracciones en
términos de su Mínimo Común Denominador (MCD).
- En este caso el MCD es 6, por lo tanto ambas fracciones pueden ser expresadas con denominador 6.
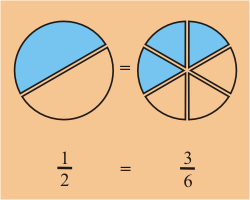 ,
, 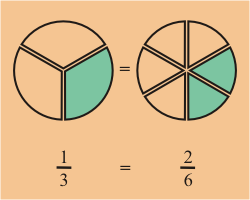
-
Ahora que los dos denominadores
son iguales, las dos fracciones se pueden sumar.
Práctica:
Resta de fracciones
El restar fracciones con el mismo denominador resulta sencillo. A estas fracciones se les conoce como fracciones homogéneasEjemplo 1:
Ejemplo 2:
La operación de resta cuando tenemos fracciones homogéneas consiste simplemente en restar los numeradores (partes del todo).
Sin embargo, si las fracciones son heterogéneas, o sea tienen distintos denominadores el proceso no es tan simple.
Ejemplo:
Podemos visualizar la cantidad que refleja la diferencia facilmente. Sin embargo, expresar dicha diferencia es más difícil.
De nuevo, si recordamos que las fracciones pueden ser expresadas en múltiples formas, o sea formas equivalentes, podremos solucionar este problema.
Un método para hallar la solución de :
-
Encuentre fracciones equivalentes
usando los denominadores posibles.
-
Seleccione el denominador común más pequeño a ambas expansiones y exprese las fracciones en términos de su Mínimo Común Denominador (MCD).
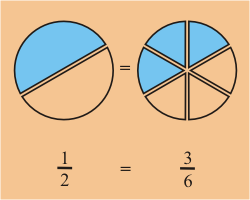 ,
, 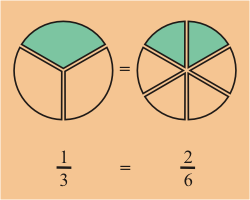
-
Ahora que los dos denominadores
son iguales, las dos fracciones se pueden restar.
Multiplicación de fracciones
Multiplicación de una fracción por un número enteroYa sabemos que
es decir,
El mismo principio se utiliza en las fracciones.
Por ejemplo, 2 × se resuelve de la siguiente manera:
Multiplica el resultado por 2:
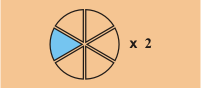
Esto es igual a añadir los dos pedazos:
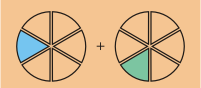
El resultado es

Que simplificado es
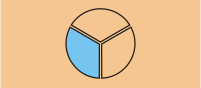
Similarmente, 3 × a = a + a + a. So 3 × puede ser resuelto de la siguiente manera:
Multiplica la fracción por 3:
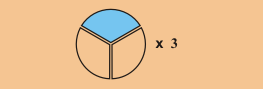
Esto es igual a añadir los tres pedazos:
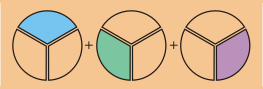
El resultado es

Que simplificado es 1

Esto puede ser generalizado a: k × = × = =
Multiplicación de una fracción porEn la sección anterior vimos que:
Por lo tanto, multiplicar por es lo mismo que tomar de la cantidad. Podemos usar esto para resolver × de la siguiente manera:

Esto puede ser generalizado a: × = = .
Multiplicación de dos fracciones ×
Si nosotros multiplicamos una cantidad
por una fracción , ésta puede ser percibida como una combinación de dos pasos anteriores:
Primero, dividimos la cantidad en b partes y entonces la multiplicamos por a.
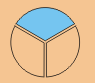
Por ejemplo, para resolver , podemos comenzar con , dividirlo por 3 y luego multiplicar el resultado por 2 de la siguiente manera:
Se corta el pastel en 2:
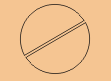
Se toma uno de los pedazos:
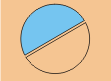
Ahora se quiere de eso. Lo dividimos en tres partes iguales y resulta ser de todo el pastel.
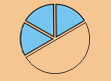
Observe la figura
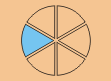
Por lo tanto = × =
.
Entonces se multiplica el resultado por 2:

Esto es igual a sumar los dos pedazos:

El resultado es

Que al simplificar es

Por lo tanto .
Para resolver podemos primero tomar una mitad de dos tercios y luego multiplicar el resultado por 3 de la siguiente manera:
Se corta el pastel en 3:
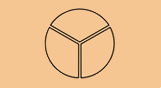
Se toman dos de los pedazos:
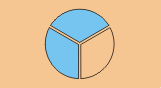
Se quiere (la mitad) de esos pedazos

Lo cual es igual a del pastel
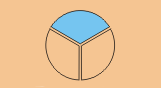
Por lo tanto, × = .
Ahora se multiplicará por 3:

Esto es igual que añadir los tres pedazos:

El resultado es

Que al simplificar es 1

Todo este proceso equivale a .
Observando estos ejemplos, se puede generalizar que:
División de fracciones
División por
De la sección pasada se sabe que:
En general, dividir por es lo mismo que multiplicar por
.
- Si una finca produce 400 plátanos cada 4 cuerdas, entonces produce
400 ÷ 4 = 100 plátanos por cuerda. - Si produce 400 plátanos cada 2 cuerdas,entonces produce 400 ÷ 2 = 200 plátanos por cuerda.
- Si produce 400 plátanos cada cuerda, entonces hay
400 ÷ = 800 plátanos por cuerda. Por lo tanto dividir por es lo mismo que multiplicar por . - Si produce 400 plátanos cada cuerda, entonces hay
400 ÷ = 1200 plátanos por cuerda. Por lo tanto dividir por es lo mismo que multiplicar por .
Tras haber visto que dividiendo por es lo mismo que multiplicar por , y que dividiendo por es lo mismo que multiplicar por , llegamos a la siguiente generalización:
Ejemplos:
Práctica: