Objetivos:
- Calcular volúmenes y áreas de superficies de sólidos geométricos: rectangulares, cilindros y esferas..
Introducción
Introducción
Existen objetos que no se pueden ubicar en el plano, como por ejemplo, una caja de cartón, una columna de concreto, un tanque de agua, una bola de baloncesto, etc. Por esta razón es necesario analizar la forma y extensión de los objetos, ubicados en el espacio, lo que se puede hacer representándolos mediante figuras geométricas y es conocida como "geometría del espacio."
Sólidos Son objetos tridimensionales y se ubican en el espacio.
Volumen Es la capacidad que ocupa un sólido en el espacio tridimensional . Volumen es el número de
unidades cúbicas que contiene.
Area de superficie Es la suma de las áreas de superficie de un sólido.
Volumen de sólidos rectangulares
Sólidos rectangulares tienen seis superficies rectangulares con tres pares de superficies paralelas que tienen las mismas medidas.
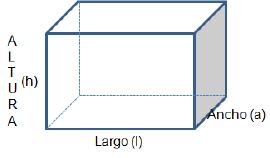
El volumen es igual al producto de largo por ancho por altura, es decir:
El área de la superficie de un sólido rectangular es igual a la suma del al área de los seis rectángulos que cubren al sólido, y que son iguales dos a dos (los que se oponen) y es dada por:
El cubo es un caso especial de los sólidos rectangulares, en el cual el largo, ancho y altura tienen la misma dimensión.
Ejemplos
1. Encuentre el volumen y el área de la superficie de un sólido rectangular cuyas dimensiones son: largo 6, ancho 4, y altura 5.
|
|
2. Si el área de la superficie de un cubo es 150 pulgadas cuadradas, determine el lado del cubo y su volumen.
|
Como la longitud es positiva se tiene que el lado del cubo mide 5 pulgadas. |
Volumen del cilindro
Cilindros o sólidos circulares son objetos tridimensionales que tienen dos círculos idénticos en planos paralelos conectados por el conjunto de todos los segmentos de rectas entre los dos círculos. Si los segmentos que unen los centros de los círculos son perpendiculares a los planos de los círculos, el cilindro se llama cilindro circular recto.
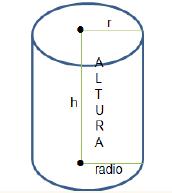
|

|
| Cilindro circular recto | Corte vertical de un cilindro circular recto |
El volumen de un cilindro que tiene dos bases circulares congruentes con área y altura es:
El área total de superficie de un cilindro circular recto es igual a la suma de área del rectángulo que se obtiene al realizar un corte vertical más las dos áreas de las bases circulares, y es dada por:
Utilice esta aplicación para encontrar el volumen y la superficie de un cilindro circular recto. Ajuste la altura y el radio con los deslizadores. Los deslizadores de varios colores se pueden utilizar para comprobar su trabajo.
Ejemplos
1. Determine el volumen y el área total de superficie de un cilindro circular recto cuya altura es de 12 pies y el radio de la base es de 2 pies.
|
|
2. Determine el volumen de un cilindro circular recto cuya altura es de 4 pies si su área total de superficie es de 24 π pies cuadrados.
|
Sustituyendo el valor de h en el área de la superficie se tiene: , dividiendo por se obtiene: |
Volumen de la esfera
Una esfera es el conjunto de todos los puntos en el espacio que son equidistantes de un punto fijo llamado centro. La distancia es el radio de la esfera. Como una esfera no tiene bases, su área es llamada su área de superficie.
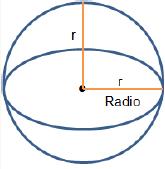
|
| Esfera de radio r |
El volumen de la esfera de radio r, es dado por:
El área de superficie de la esfera de radio r, es dada por:
Utilice esta aplicación para encontrar el volumen y la superficie de un cilindro circular recto. Ajuste la altura y el radio con los deslizadores. Los deslizadores de varios colores se pueden utilizar para comprobar su trabajo.
Ejemplos
1. Si el radio de una esfera es de 3 pies, determine su volumen y área de superficie.
|
|
2. La circunferencia promedio de la tierra es aproximadamente 24,900 millas. ¿Cuáles son los valores aproximados de su superficie y volumen?
|
y podemos considerar su radio como 3,963 millas. |
Práctica
Presione el boton para practicar ejercicios de geometría del espacio

Resumen
Ahora que has terminado esta lección debes ser capaz de:
- Calcular volúmenes y áreas de superficies de sólidos geométricos: rectangulares, cilindros y esferas.
File applications developed with GeoGebra