Geometría1. Objetivos
2. IntroducciónEl estudio de la geometría debe incluir experiencias y actividades que les permita a los estudiantes entender el signi ficado de la geometría en sus vidas del diario vivir. Es importante que los estudiantes desarrollen habilidades inductivas usando manipulativos o programado de computadoras. Además es importante el aprendizaje en grupo que les permita discutir la solución de los problemas y las conexiones de la geometría con las otras disciplinas como álgebra y cálculo. La geometría es muy importante debido a que permite enseñar y aprender el arte de razonar, porque es abstracta, pero fácil de visualizar y tiene muchas aplicaciones concretas como por ejemplo, calcular el área de un lote a ser cercado, determinar el volumen de un lata que contiene refresco, construir puentes bien estructurados, estaciones experimentales en el espacio, grandes coliseos deportivos, etc. A continuación se muestra la iglesia de Santa Sofía construída en los años 300, pertenece a la arquitectura Bizantina y fue diseñada usando figuras geométricas, como semiesferas, rectángulos. 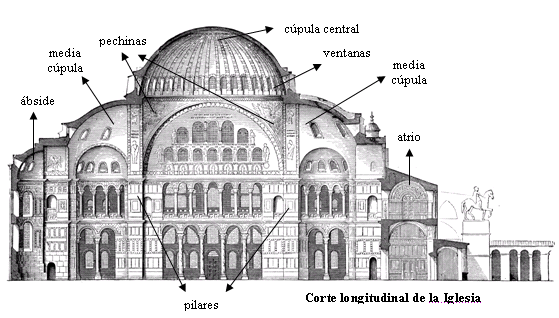 http://www.monografias.com/trabajos55/iglesia-santa-sofia/Image13780.gif La geometría elemental se divide en dos partes, geometría plana (estudia la figuras planas, que tienen únicamente dos dimensiones: largo y ancho) y geometría del espacio (estudia las propiedades de los cuerpos geométricos provistos de largo, ancho y altura o profundidad). 3. Geometría plana
La geometría plana estudia las fi
guras planas, que tienen únicamente dos dimensiones: largo y ancho. 3.1 Conceptos básicos de geometríaPara el estudio de la geometría, es indispensable conocer el concepto intuitivo de punto, recta y plano. Estos son términos no definidos que proveen el inicio de la geometría. Punto es el objeto fundamental en geometría, el punto representa solo posición y no tiene dimensión, es decir, largo cero, ancho cero y altura cero. Se representan por letras mayúsculas. Ejemplo: Tres puntos  Recta tiene solo longitud, no tiene ancho ni altura ni grosor. Es un conjunto in finito de puntos que se extienden en una dimensión en ambas direcciones. Una recta se puede representar por:  Plano tiene ancho y largo, sin altura ni grosor. Un plano es una superfi cie en dos dimensiones, se puede pensar como un conjunto de puntos in finitos en dos dimensiones.  3.2 PolígonosUn polígono es una fi gura plana cerrada que está formada por tres o más segmentos de recta que se unen en sus puntos extremos. Los segmentos de recta que forman un polígono solo se intersectan en sus puntos extremos. Los polígonos se nombran de acuerdo al número de lados que están formados.
Ejemplos de polígonos:
Las partes de un polígono son: 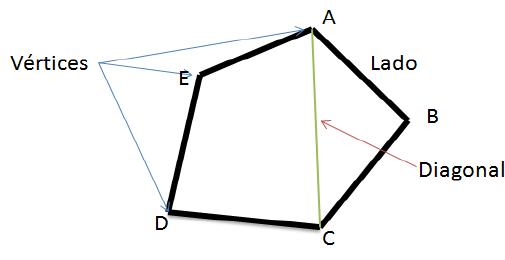 Vértices: puntos finales de los segmentos que forma el polígono, en la fi gura: A, B, C, D, E. Lados: segmentos de recta que unen dos vértices consecutivos del polígono, en la fi gura los lados son: AB, Lados consecutivos: cualquier par de lados que comparten un vértice, en la figura: AB y BC, BC y CD, Diagonal: un segmento de recta que une dos vértices no consecutivos, en la figura: AC.
3.3 Perímetro y áreas de polígonosEl perímetro de un polígono es la suma de la longitud de cada uno de los lados. Las unidades para el perímetro representan longitud o distancia, y son singulares por que tiene una sola dimensión. Las unidades de longitud son: pulgadas, pies, millas, centímetros, metros, kilometros, etc.El área de un polígono es la medida interna en dos dimensiones de su super ficie plana. Las unidades de área representan dos dimensiones y son cuadradas y son: pies cuadrados (pies ), metros cuadrados (m ) unidades especiales como cuerdas, para medir las superfi cies de las fincas, etc. A continuación se discuten el perímetro y área de algunos polígonos especiales:
3.3.1 TriánguloUn triángulo es un polígono que es una porción del plano limitado por tres rectas que se cortan dos a dos y que tiene tres lados y tres ángulos. 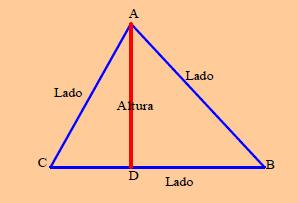 Altura es la perpendicular trazada desde un vértice, al lado opuesto o a su prolongación, en la figura anterior es el segmento DA.
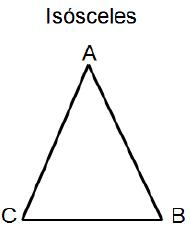
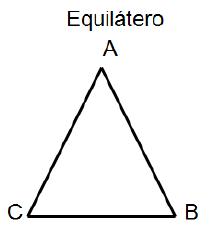
Clasificación de triángulos:
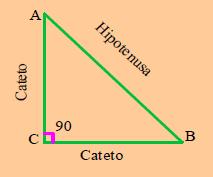 Teorema La suma de los ángulos interiores de un triángulo valen dos ángulos rectos. Teorema de Pitágoras En todo triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual
a la suma de los cuadrados de las longitudes de los catetos. donde AB,BC y CA representan la longitud de los lados AB, BC y CA, respectivamente. El área de un triángulo se defi ne como la mitad del producto de la longitud de la base por la longitud de la altura, es decir: donde BC y DA representan la longitud de la base BC y la longitud de la altura DA, respectivamente. Ejemplos: 1. Considere los siguientes triángulos para determinar el perímetro y área de cada uno de ellos: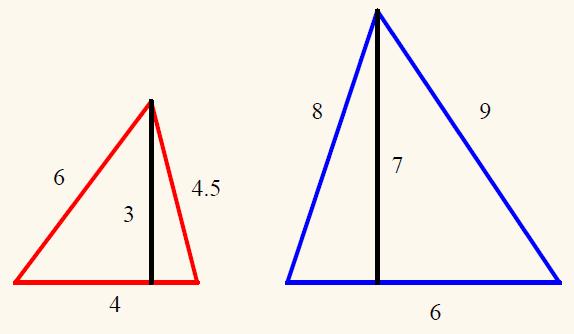
2. Si el área de un triángulo es 12 cm y su altura es 4 cm, determine la base del triángulo.
3. Si el perímetro de un triángulo rectángulo isósceles es 22 y la longitud de su hipotenusa es 10, halle el área del triángulo rectángulo.
4. ¿Puede ser equilátero un triángulo rectángulo?
Ejercicios: 
3.3.2 CuadriláterosLos cuadriláteros son polígonos de 4 lados y se clasi fican de acuerdo al paralelismo de sus lados opuestos. Si los lados opuestos son paralelos se llaman paralelogramos, ver la siguiente figura:
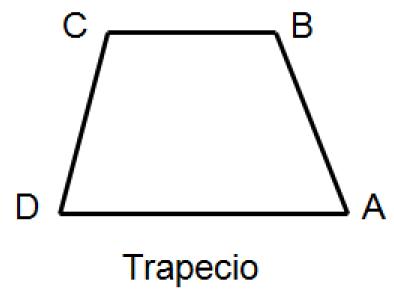
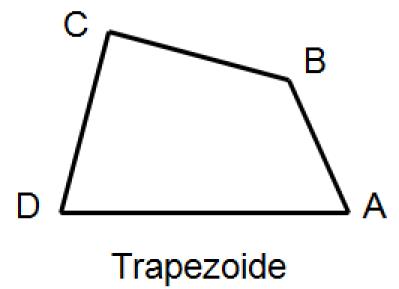
Cuando solo hay paralelismo en un par lados opuestos, se le llama trapecio. Si no existe paralelismo, se le llama trapezoide, ver la siguiente figura:
Rectángulo: Tiene los cuatro ángulos rectos y los lados consecutivos desiguales. 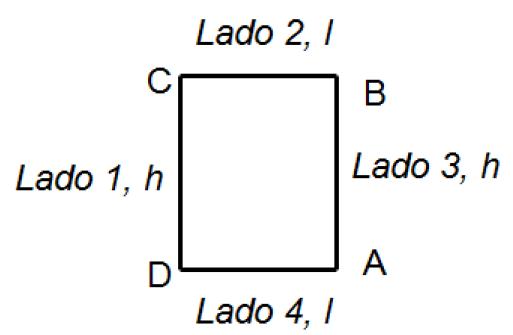 El perímetro del rectángulo es la suma de sus cuatro lados, o equivalentemente, dos veces el largo más dos veces el ancho, es decir: Perímetro = Lado1+Lado2+Lado3+lado4 Area del rectángulo es el producto de su largo por su ancho, es decir:
Cuadrado: Tiene los cuatro ángulos rectos y los lados iguales. 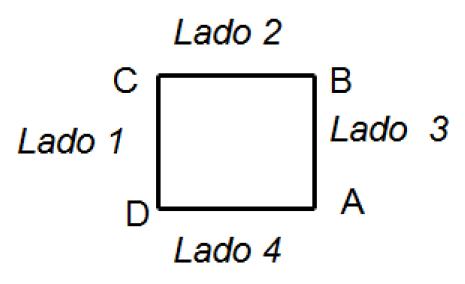
El perímetro del cuadrado es la suma de sus cuatro lados, o equivalentemente, cuatro veces la longitud de un lado, es decir: Perímetro = Lado1+Lado2+Lado3+lado4=4(Lado1) El área del cuadrado es el cuadrado de la longitud de uno de sus lados, es decir:
Paralelogramo: Es el cuadrilátero que tiene sus lados opuestos paralelos dos a dos. El paralelogramo tiene altura que es el segmento perpendicular a ambos lados opuestos y paralelos. 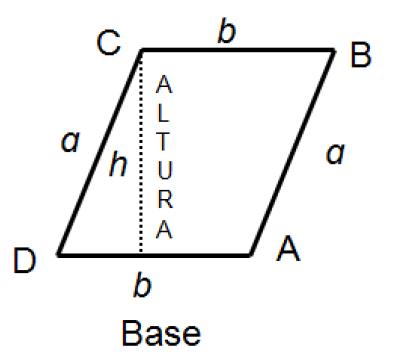 El perímetro del paralelogramo es la suma de las longitudes de sus cuatro lados, o equivalentemente, dos veces un lado paralelo más dos veces el otro lado paralelo, es decir:
El área del paralelogramo es el producto de su base por la altura correspondiente a dicha base, es decir:
Trapecio Es el cuadrilátero que tiene solamente un par de lados paralelos, que se llaman bases. El paralelogramo tiene altura que es el segmento perpendicular a ambos lados opuestos y paralelos. 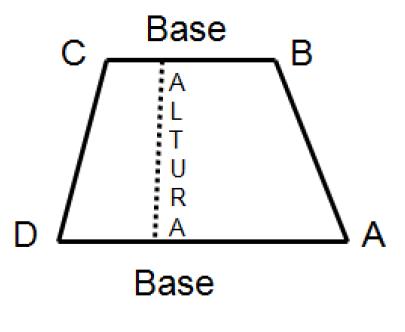 El perímetro del trapecio es la suma de sus cuatro lados, o equivalentemente, dos veces su base más la suma de los lados no paralelos, es decir: Perímetro El área del trapecio es el promedio de sus bases por la altura, es decir:
Ejemplos: 1. Halle los valores de x e y para que el cuadrilátero que se muestre sea un paralelogramo y luego determine su perímetro. 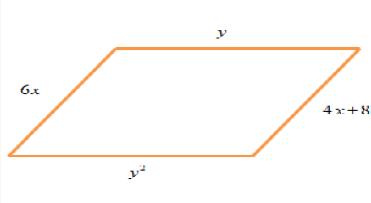
2. Dado el siguiente rectángulo, si el perímetro es 58, determine el valor de x y luego su área. 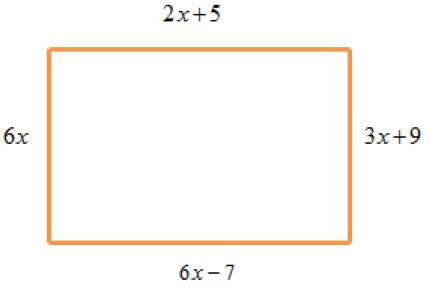
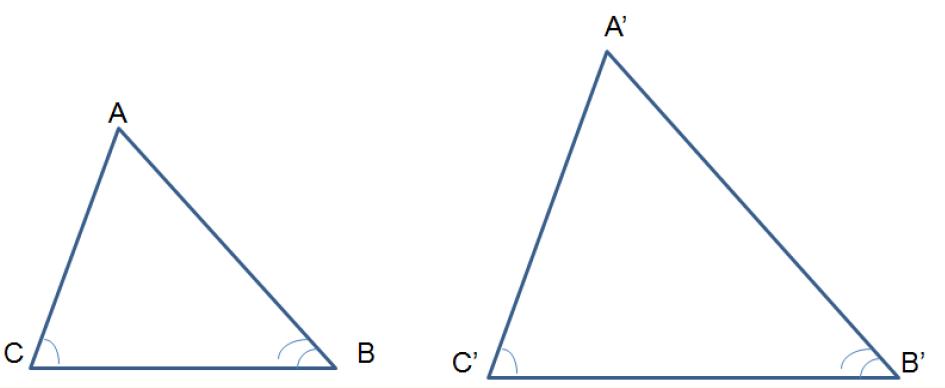
Ejercicios:  3.4 Semejanza de triángulosDos triángulos son semejantes cuando tienen sus ángulos respectivos de igual medida y sus lados son proporcionales. El signo de semejanza es ˜ :
Si y , entonces Definición dos lados son homólogos si se oponen a ángulos de igual medida. En la figura anterior, los lados y y y y , son homólogos.Criterios de semejanza de triángulos Caso 1. Si tiene dos ángulos respectivamente iguales. Caso 2. Si tiene dos lados proporcionales y el ángulo comprendido es igual.
Caso 3. Si tiene sus tres lados proporcionales. Ejemplos 1. En los siguientes triángulos, si y halle y 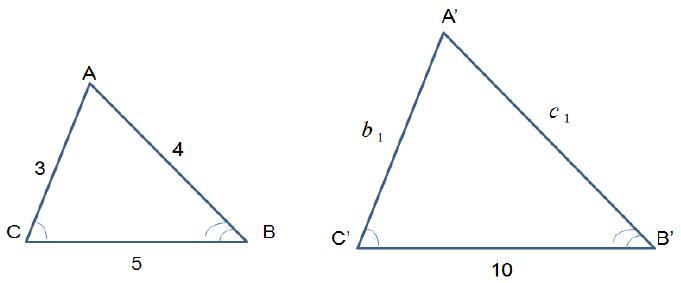
2. Dados los siguientes triángulos, son semejantes?: 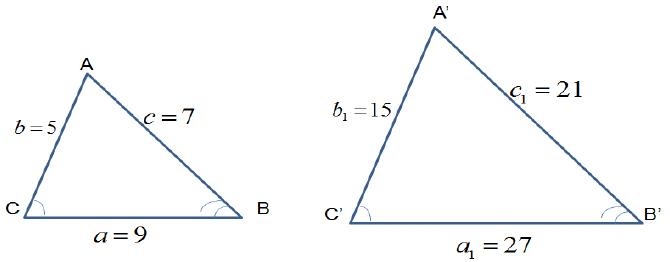
3. Dado que AB es paralelo a DE y los segmentos AE y BD se intersectan en el punto C, determine si los triángulos ABC y CDE son semejantes y si los son halle la longitud del lado AC. 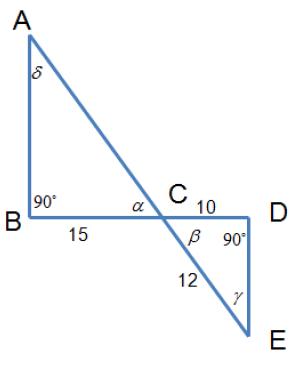
Ejercicios:  3.5 Círculos: perímetro y áreaDefi nición es una figura plana que consiste de todos los puntos que están sobre una curva cerrada y de los puntos interiores de ella, en la cual cada punto sobre la curva tiene la misma distancia al centro del círculo. 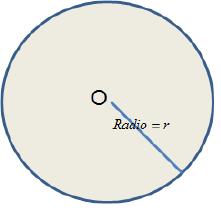 Radio de un círculo es la distancia entre el centro y cualquier punto de la curva y tiene longitud r: Diámetro de un círculo es la distancia entre dos puntos cualesquiera de la curva cerrada y que pasa por el centro y tiene longitud d = 2r y divide a un círculo en dos partes iguales: Perímetro de un círculo es llamado circunferencia y se define por donde r es el radio, d el diámetro y Area de un círculo con radio r y diámetro d es Ejemplos 1. Determine la circunferencia de un círculo si su área es 36 π metros cuadrados.
2. Halle la circunferencia y área del círculo que se muestra a continuación: 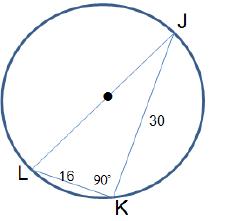
Ejercicios:  3.6 Areas combinadasEl objetivo es determinar las áreas de regiones que resultan de la combinación de otras figuras planas conocidas como: triángulos, rectángulos, trapecios y círculos. Ejemplos 1. Hallar el área del trapecio ABCD; si el área del triángulo ABH es 8m además m 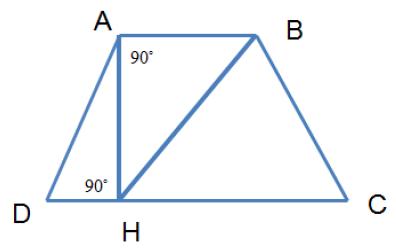
2. Determine el área del triángulo AFD si m, y m. 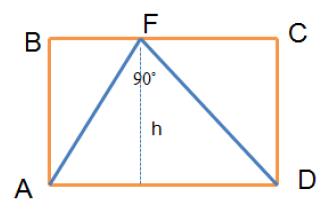
3.Determine el área de la región sombreada 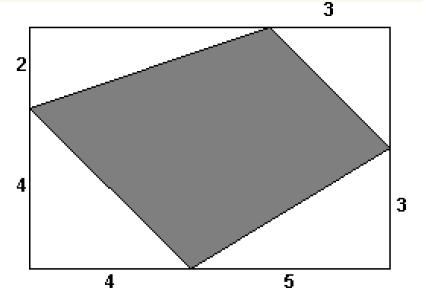
4. En la siguiente figura determine el área de la región sombreada si cm. 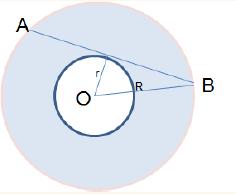
Ejercicios:  4. Geometría del espacioExisten objetos que no se pueden ubicar en el plano, como por ejemplo, una caja de cartón, una columna de concreto, un tanque de agua, una bola de baloncesto, etc. Por esta razón es necesario analizar la forma y extensión de los objetos, ubicados en el espacio, lo que se puede hacer representándolos mediante figuras geométricas y es conocida como "geometría del espacio." Sólidos Son objetos tridimensionales y se ubican en el espacio. 4.1 Volúmen de sólidos rectangularesSólidos rectangulares tienen seis super ficies rectangulares con tres pares de superfi cies paralelas que tienen las mismas medidas. 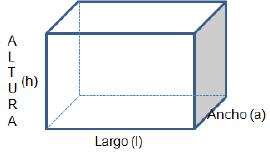 El volumen es igual al producto de largo por ancho por altura, es decir:
El área de la superfi cie de un sólido rectangular es igual a la suma del al área de los seis rectángulos que cubren al sólido, y que son iguales dos a dos (los que se oponen) y es dada por:
El cubo es un caso especial de los sólidos rectangulares, en el cual el largo, ancho y altura tienen la misma dimensión.
Ejemplos 1. Encuentre el volumen y el área de la superfi cie de un sólido rectangular cuyas dimensiones son: largo 6, ancho 4, y altura 5.
2. Si el área de la superfi cie de un cubo es 150 pulgadas cuadradas, determine el lado del cubo y su volumen.
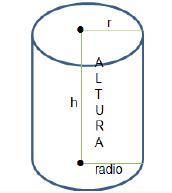
4.2 Volúmenes de cilindrosCilindros o sólidos circulares son objetos tridimensionales que tienen dos círculos idénticos en planos paralelos conectados por el conjunto de todos los segmentos de rectas entre los dos círculos. Si los segmentos que unen los centros de los círculos son perpendiculares a los planos de los círculos, el cilindro se llama cilindro circular recto.
El volumen de un cilindro que tiene dos bases circulares congruentes con área y altura es:
El área total de superfi cie de un cilindro circular recto es igual a la suma de área del rectángulo que se obtiene al realizar un corte vertical más las dos áreas de las bases circulares, y es dada por:
Ejemplos 1. Determine el volumen y el área total de superfi cie de un cilindro circular recto cuya altura es de 12 pies y el radio de la base es de 2 pies.
2. Determine el volumen de un cilindro circular recto cuya altura es de 4 pies si su área total de superfi cie es de 24 π pies cuadrados.
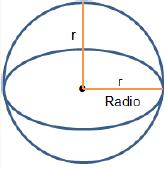
4.1 Volúmen de sólidos rectangularesUna esfera es el conjunto de todos los puntos en el espacio que son equidistantes de un punto fijo llamado centro. La distancia es el radio de la esfera. Como una esfera no tiene bases, su área es llamada su área de superfi cie.
El volumen de la esfera de radio r, es dado por:
El área de superfi cie de la esfera de radio r, es dada por:
Ejemplos 1. Si el radio de una esfera es de 3 pies, determine su volumen y área de superfi cie.
2. La circunferencia promedio de la tierra es aproximadamente 24,900 millas. ¿Cuáles son los valores aproximados de su superfi cie y volumen?
Ejercicios:  |