Al concluir esta lección, deberás ser capaz de:
- Identificar si dos lineas son paralelas.
- Identificar si dos lineas son perpindiculares.
- Identificar y conseguir la formula de rectas verticales.
- Reconocer y usar formulas diferentes de una relacion lineal.
En la lección de Ecuaciones Lineales - Parte 1, vimos que
es una recta con pendiente m e intercepto b. A continuación exploraremos varias relaciones entre rectas y varias alternativas para representar rectas distintas de y = mx + b.
Dos rectas paralelas se pueden describir en una variedad de maneras:
- Dos rectas en un plano que jamás se intersecan.
- Dos rectas que mantienen una distancia constante entre ellas.
- Dos rectas con pendientes iguales.
Para resolver problemas matemáticos, generalmente lo mas fácil es caracterizar rectas paralelas como dos rectas con pendientes iguales.
Ejemplos:
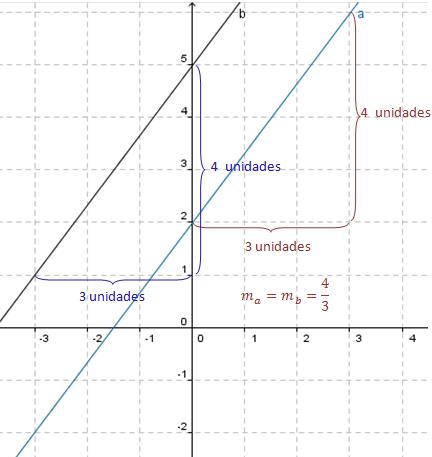
Ejemplo 1: Las rectas
y
son paralelas.
Ejemplo 2: Sigue las instrucciones a continuación en la aplicación siguiente y observa los efectos de distintos cambios en las fórmulas en las gráficas de las rectas:
- Mueve el botón m1 hasta que las dos rectas sean paralelas
- Ahora, mueve el botón b1 desde b1 = -5 hasta b1 = 5. Cambiar el intercepto b1 no cambia la pendiente de la recta. Así el valor del intercepto no tiene ningún efecto en si las rectas son o no paralelas. Si las pendientes de las dos rectas son iguales, entonces las rectas son paralelas.
- Mueve los botones rojos hasta cambiar la fórmula de la recta 1 a y = 2x +1. Luego mueve los botones azules para encontrar cuatro formulas de cuatro rectas paralelas a y = 2x + 1.
- Mueve los botones rojos hasta cambiar la fórmula de la recta 1 a y = –3x + 4. Luego mueve los botones azules para encontrar cuatro formulas de cuatro rectas paralelas a y = –3x + 4.
Ejemplo 3: Encuentra la ecuación de la recta que pasa por el punto (3,2) y es paralela a la recta
Solución:
|
1. La pendiente de es igual a 2.
|
|
2. La pendiente de una recta paralela a
tiene que ser 2 también. Así, la recta paralela debe tener una fórmula
|
3. Si la formula de la recta es y = 2x + b, todo que falta es encontrar el valor del intercepto b. Si la recta pasa por el punto (3,2), al sustituir 3 para x en la fórmula el resultado (el valor de y) tiene que ser 2. Así:
- Al sustituir 3 para x y 2 para y en la fórmula y = 2x + b, da 2 = 2×3 + b
- Ahora se puede resolver para el valor de b que hará la ecuación cierta:
2 = 6 + b
2 – 6 = b
–4 = b
|
4. Así la fórmula de la recta que pasa por el punto (3,2) y es paralela a la recta
y = 2x + 3 es
|
5. Verificación
- y = 2x + 2 y y = 2x - 4 tienen la misma pendiente 2. Por lo tanto son paralelas.
- El punto (3,2) satisface la formula y = 2x - 4 porque al sustituir 3 para x y 2 para y resulta:
2 = 2×3 - 4, lo cual es cierto.
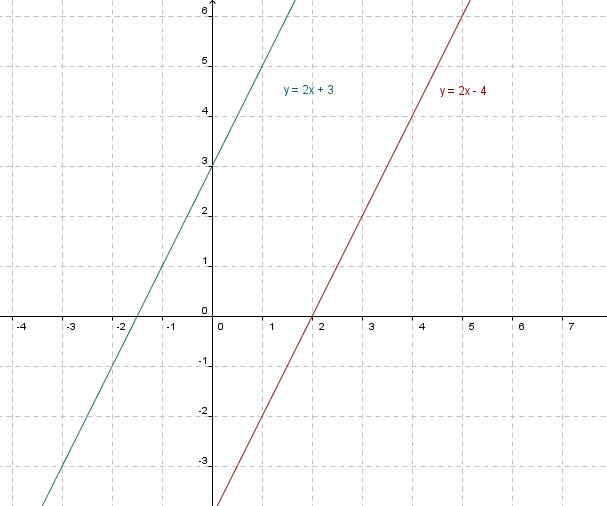
Asi y = 2x - 4 es paralela a y = 2x + 3 y pasa por el punto (3,2). Se puede visualziar con las gráficas de las dos rectas.
|

Dos rectas perpendiculares se describen con frecuencia en una de dos maneras:
- Dos rectas que forman ángulos de 90 grados donde intersecan.
- Dos rectas de un plano donde el producto de sus pendientes es –1.
Para resolver problemas matemáticos, la caracterización más utilizada es: dos rectas donde el producto de sus pendientes es –1 son perpendiculares.
Ejemplos:
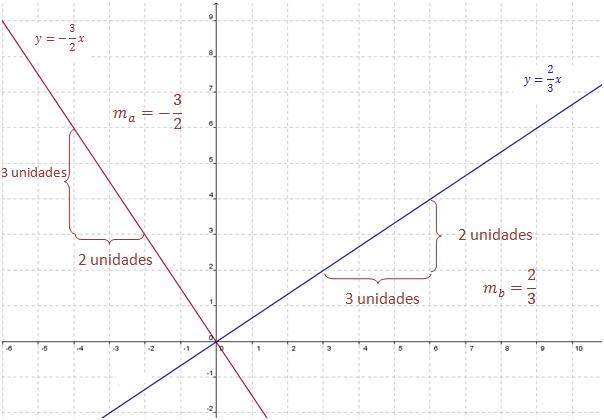
Ejemplo 1:Si la pendiente de una recta es , entonces para cada 3 que aumenta la coordenada de x mientras se mueve desde la izquierda hacia la derecha en esa recta la coordenada de y aumenta 2.
De acuerdo a la caracterización, una recta perpendicular a esa tendría pendiente . En la recta perpendicular, para cada 2 que aumenta la coordenada de x mientras que se mueve de izquierda a derecha la coordenada de y disminuye 3. (En otras palabras para cada 3 que aumenta la coordenada de y mientras que se mueve desde abajo hacia arriba, la coordenada de x disminuye 2.)
Ejemplo 2: Sigue las instrucciones a continuación en la aplicación subsiguiente y observe los efectos de distintos cambios fórmulas en las gráficas de las rectas:
- Mueve el botón m1 hasta que las dos rectas son perpendiculares
- Ahora, mueve el botón b1 desde b1 = –5 hasta b1 = 5. Cambiar el intercepto b1 no cambia la pendiente de la recta. Así el valor del intercepto no tiene ningún efecto en si las rectas son o no son perpendiculares. Si el producto de las dos pendientes es –1, entonces las rectas son perpendiculares.
- Mueve los botones rojos hasta cambiar la fórmula de la recta 1 a y = 2x +1. Luego mueve los botones azules para encontrar cuatro formulas de cuatro rectas perpendiculares a y = 2x + 1.
- Mueve los botones rojos hasta cambiar la fórmula de la recta 1 a y = –3x + 4. Luego mueve los botones azules para encontrar cuatro formulas de cuatro rectas perpendiculares a y = –3x + 4.

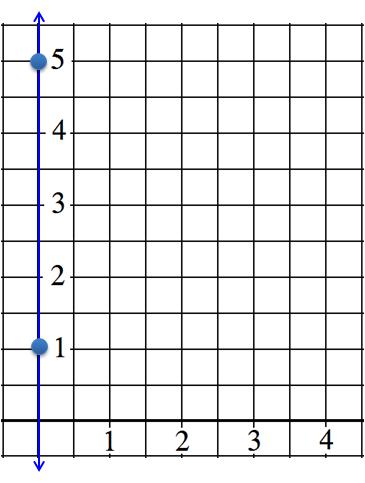
En el diagrama siguiente los dos puntos (0,1) y (0,5) están rotulados y hay una recta dibujada que pasa por los dos puntos. En la sección de Ecuaciones Lineales de Dos Variables, vimos que las pendientes se pueden expresaron en distintas formas:
- La pendiente m es igual a cuanto sube y cuando x aumenta por 1.
- m=elevación/avance=Δy/Δx
- elevación = m × avance o Δy = m × Δx
En el caso de los dos puntos (0,1) y (0,5), el valor de x es constante. Por lo tanto x jamás aumenta por 1, jamás avance y por consecuencia Δx es cero en todos los casos. Así la pendiente no se define para la recta que pasa por esos puntos. La fórmula usual de pendiente intercepto y = mx + b no sirve para representar el conjunto de puntos que pertenece a esa recta ni ninguna recta vertical. Al examinar varios puntos que pertenecen a esa recta como
(0,–1), (0,0), (0,1) y (0,2)
se observa que la coordenada de x es cero en todos y todo punto que tiene la coordenada de x cero estará en esa recta. Así una fórmula para esa recta es x = 0.
En general, con rectas verticales:
- El valor de x no cambia y la ecuación se expresa en la forma , donde a es una constante.
- Δx es igual a cero, la pendiente de una recta vertical no está definida y decimos que una recta vertical no tiene pendiente.
Ejemplos:
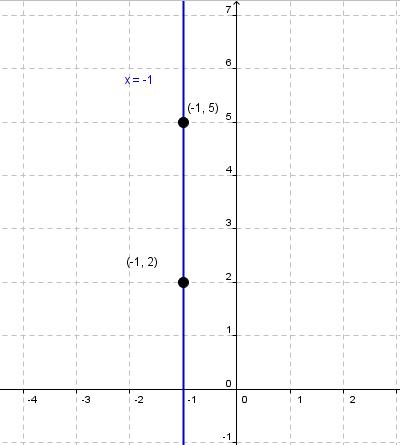
Ejemplo 1: Determinar la ecuación de la recta que pasa por los puntos (-1,2) y (-1,5)
| Dado que la primera coordenada de ambos puntos es la misma, la única posibilidad es que la recta que pasa por esos dos puntos es una recta vertical, es decir que para cualquier valor de y, el valor de x tiene que ser –1. Así la ecuación de la recta seria: x = −1.
|
Ejemplo 2: Sigue las instrucciones en la aplicación subsiguiente y observa los efectos de distintos cambios en las fórmulas en las gráficas de las rectas:
- Mueve el punto J hasta que este encima del punto (2,0). Verás la ecuación de la recta, x = 2 escrita en rojo.
- Mueve el botón azul hasta 4 para ver cuatro puntos rotulados en la recta. Verifica que los cuatro puntos satisfacen la ecuación x = 2.
- Mueve J hasta cada una de las cuatro rectas verticales x = –1, x = –3, x = 0 y x = 3. Para cada recta, verifica que los 4 puntos satisfacen la ecuación (rotulado en rojo) de la recta.

Hasta ahora, hemos usado y = mx + b para representar rectas no verticales. Esta manera de representar se llama pendiente-intercepto. Hay circunstancias en las cuales otras formas de expresar una ecuación de recta resultan más útiles:
- Punto-Pendiente: Dada una recta que pasa por (2,3) con pendiente igual a 4. Cualquier otro punto (x,y) en esa recta tiene que servir para calcular la pendiente de la recta. Como la pendiente es 4,
tiene que ser 4 o sea:
Cuando se multiplica los dos lados de la ecuación por (x – 3) resulta la forma (ecuación) conocido como Punto-Pendiente:
(y – 3) = 4(x – 2)
En general, se puede representar la recta con pendiente m que pasa por el punto (a,b) con la forma Punto-Pendiente (ecuación):
(y – b) = m(x – a)
Por costumbre escribimos las ecuaciones como formulas para calcular el valor de y al sustituir el valor de x. En ese caso la forma Punto-Pendiente sería:
y = m(x – a) + b
- Formula Estandard:
Cuando una recta se escribe ax + by = c, decimos que la ecuación está en forma estándar. La forma estándar es muy útil para encontrar los interceptos de x y de y. Por ejemplo, en el caso de la ecuación 2x +4y = 8, cuando x = 0 al sustituir 0 para x en esa ecuación sale en seguida 4y = 8 y por tanto y = 2 es el intercepto del eje de y. Cuando y = 0, al sustituir 0 para y en la ecuación sale en seguida 2x = 8 y por tanto x = 4 es el intercepto del eje de x es 4. Con los dos interceptos (0,2) y (4,0) se puede dibujar la gráfica de la recta de forma eficiente. Vea la gráfica a continuación y confirma que todos los puntos en la recta satisfacen la ecuación 2x +4y = 8.
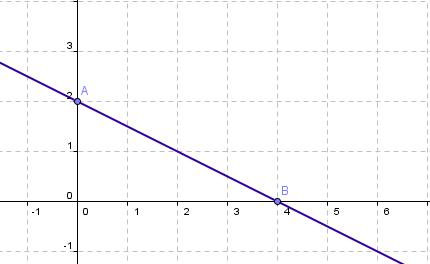
En general, si ax + by = c, los interceptos son de la forma
y
.
Para practicar representar rectas en varias formas, sigue las instrucciones a continuación en la aplicación subsiguiente.
- Con los botones azules, selecciona m = -1 y b = 20. La gráfica que resulta debe ser y = –1x + 20 con pendiente -1 e intercepto en el eje de y de (0,20).
- Oprime la caja al lado del texto verde rotulado Punto-Pendiente. Mueve el punto verde en la recta rotulado P a los puntos siguientes. Anota la fórmula de forma Punto-Pendiente asociado con cada punto.
| P |
Formula Punto-Pendiente Asociada | Formula Punto-Pendiente Asociado
|
| (20,0) | (y – 0) = –1(x – 20) | y = –1(x – 20) + 0 |
| (0,20) | (y – 20) = –1(x – 0) | y = –1(x – 0) + 20 |
| (-20,40) | (y – 40) = –1(x + 20) | y = –1(x + 20) + 40 |
- Verifica que todas las fórmulas resultantes son equivalentes a la formula Pendiente-Intercepto y =–x + 20.
- Oprime la caja al lado del texto rojo que rotulado Forma Estándar. Con los botones rojos, selecciona los interceptos L = 20 y M = 20. Verifica que la recta que tiene los interceptos (0,20) y (20,0) es idéntica a la recta vista en los pasos anteriores y que su forma estándar es x + y = 20 es equivalente a la fórmula Pendiente-Intercepto:
y = –x + 20
- Para practicar, utiliza la aplicación para expresar las siguientes rectas con fórmulas en forma Punto-Pendiente y en forma estándar:
| a. y = -2x + 40 |
b. y = 2x - 30 |
c. y = -5x + 30 |
d. y = 6x - 20 |

|
Ahora que has completado esta lección, eres capaz de:
- Identificar si dos rectas son paralelas.
- Identificar si dos rectas son perpendiculares.
- Identificar y conseguir la fórmula de rectas verticales.
- Reconocer y usar distintas fórmulas para representar una relación lineal.
|
|