Multiplicación de Binomios y Polinomios
Objetivos
Al término de esta lección, debe ser capaz de:
- Multiplicar dos binomios y reconocer como ese producto se puede visualizar usando el área de un rectángulo.
- Reconocer los casos especiales:
- (ax + b)2
- (ax - b)2
- (ax + b)(ax - b)
- Multiplicar dos polinomios y reconocer como ese producto se puede visualizar usando el área de un rectángulo.
Introducción
Supongamos que una familia está considerando ampliar el tamaño de su casa, donde el ancho actual es de 12 metros
y su largo actual es 10 metros.
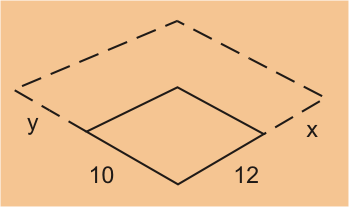
La familia aún no está segura de cuánto desean ampliar la casa por lo que asumen que el ancho se ampliará
en metros y que su largo se extenderá en
metros.
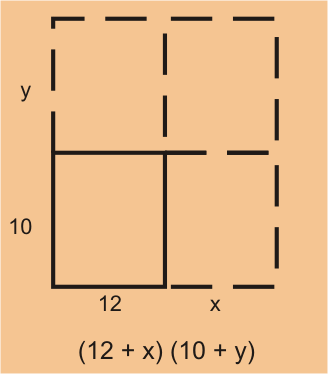
El nuevo ancho de la casa será
y el nuevo largo de la casa será . La nueva área de la casa, por lo tanto, estará
dada por la fórmula Área
ó
Área .
Para enfrentar estas situaciones, tenemos que ser capaces de multiplicar expresiones tales como
.
Producto de Sumas
Ejemplo 1: Encuentre el producto de
.
Solución: Esto puede ser visualizado de mejor manera en el siguiente rectángulo.
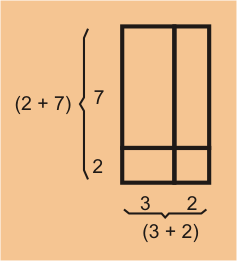 Hay dos enfoques para este problema:
Hay dos enfoques para este problema:
- El primer método consiste en hallar el área del rectángulo grande.
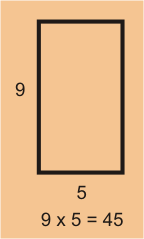
Usando esta tácnica, el área correspondiente es
.
- El segundo método consiste en encontrar el área de todos los rectángulos internos y sumarlos.
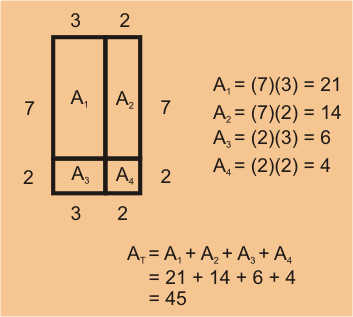
En este caso, el área es igual a .
Como el área de un mismo rectángulo no puede cambiar, los dos enfoques dan la misma respuesta.
Luego en términos de la multiplicación de expresiones binomiales, podemos concluir que
.
Ejemplo # 2: Encontrar el producto de .
Solución: Esto se puede visualizar mejor en el siguiente rectángulo.
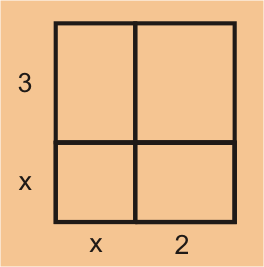 Hay dos enfoques de este problema:
Hay dos enfoques de este problema:
- El primer método para obtener el producto se da al encontrar el área del rectángulo grande.
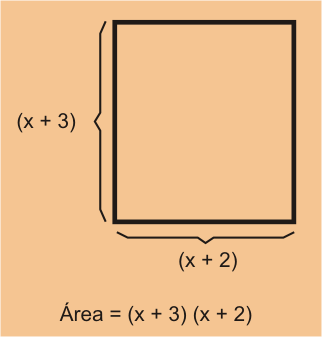
Usando esta técnica, la fórmula para el área asociada es:
Área ,
la cual no se puede simplificar.
- El segundo método consiste en encontrar el área de todos los rectángulos internos y sumarlos.
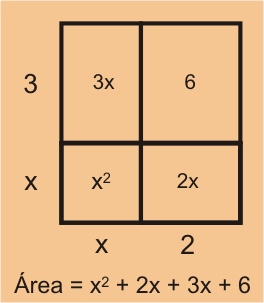
En este caso, la fórmula para el área asociada es:
Área .
Como el área de el mismo rectángulo no puede cambiar, los dos enfoques dan la misma respuesta. Por lo tanto, podemos concluir que
.
Ejemplo # 3: Encuentre el producto de .
Solución: Esto se visualiza mejor en el siguiente rectángulo .
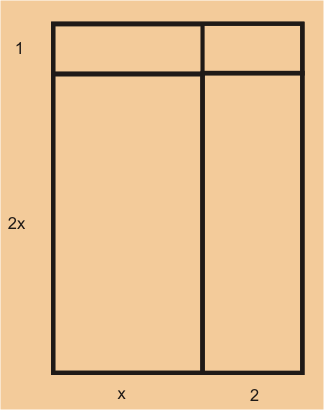 Hay dos enfoques de este problema:
Hay dos enfoques de este problema:
- El primer método para obtener el producto consiste en encontrar el área del rectángulo grande.
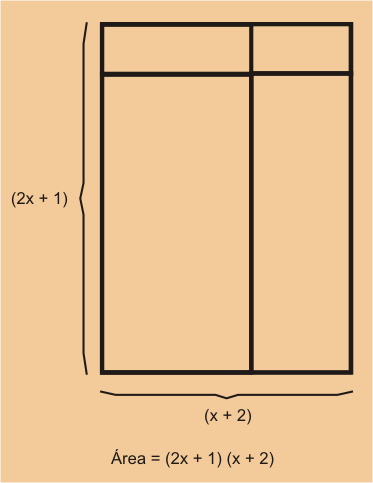
Usando esta técnica, la fórmula para el área asociada es
Área ,
que no se puede simplificar.
- El segundo método es encontrar el área de todos los rectángulos internos y sumarlos.
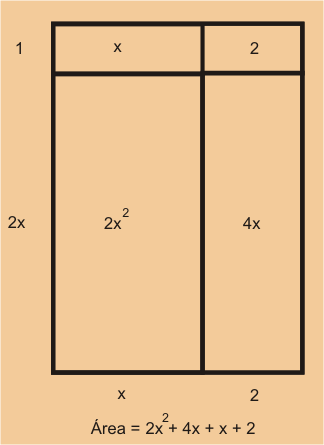
En este caso, la fórmula para el área asociada es:
Área .
Como el área de un mismo rectángulo no se puede cambiar, los dos enfoques dan la misma respuesta.
Por lo tanto, podemos concluir que:
.

Productos de Diferencias
Podemos visualizar la geometría de las diferencias de una manera similar a la suma.
Ejemplo:
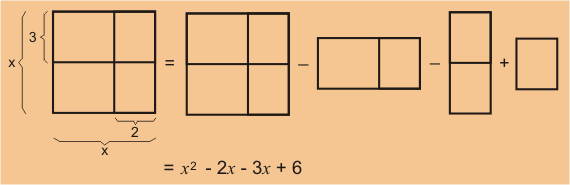 Sin embargo, un método más simple es asumir que los negativos se pueden adicionar como los otros números.
Ejemplo # 1: Encuentre el producto
Solución: En primer lugar, volvamos a escribir la diferencia como
.
Sin embargo, un método más simple es asumir que los negativos se pueden adicionar como los otros números.
Ejemplo # 1: Encuentre el producto
Solución: En primer lugar, volvamos a escribir la diferencia como
.
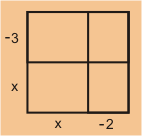 Hay dos enfoques de este problema:
Hay dos enfoques de este problema:
- El primer método para obtener el producto se da al encontrar el área del rectángulo grande.
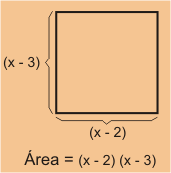
Usando esta técnica, la fórmula para el área asociada es
Área la cual no se puede simplificar.
- El segundo método es encontrar el área de todos los rectángulos internos y sumarlos.
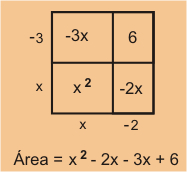
En este caso, la fórmula para el área asociada es:
Área .
Como el área de un mismo rectángulo no se puede cambiar, los dos enfoques dan la misma respuesta.
Por lo tanto, podemos concluir que:
.
Ejemplo # 2: Encontrar el producto
Solución: En primer lugar, volvamos a escribir la diferencia como
Hay dos enfoques de este problema:
- El primer método para obtener el producto se da al encontrar el área del rectángulo grande.
Usando esta técnica, la fórmula para el área asociada es:
Área ,
la cual no se puede simplificar.
- El segundo método es encontrar el área de todos los rectángulos internos y sumarlos.
En este caso, la fórmula para el área asociada es:
Área .
Como el área de un mismo rectángulo no se puede cambiar, los dos enfoques dan la misma respuesta.
Por lo tanto, podemos concluir que:
.

Casos Especiales
Ya hemos visualizado las geometrías tanto del producto, las sumas como de las diferencias. Ahora veremos algunos casos especiales. El primer caso especial es cuando el producto es de dos expresiones iguales, sean dos sumas o dos diferencias, y para esto utilizaremos el segundo método de los rectángulos de la sección anterior.
Caso # 1:
: el cuadrado de una suma
Cuando multiplicamos una suma por sí misma, podemos decir que estamos buscando el cuadrado de la suma.
Geométricamente, el área del cuadrado de una suma es representada por un cuadrado, ya que todo cuadrado es un rectángulo.
Ejemplo # 1: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.
En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ejemplo # 2: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.
 En este caso, la fórmula para el área asociada es:
En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ambas soluciones tienen algo en común:
-
Su primer término es el cuadrado de el primer término de la suma,
- El término del medio es el doble del producto de los dos términos que componen la suma y
- El último término de la solución es el cuadrado del último término de la suma.
Por tanto, podemos crear una regla general para todos los cuadrados de una suma:
Caso # 2:
: el cuadrado de una diferencia
Cuando multiplicamos una diferencia por sí misma, podemos decir que estamos buscando el cuadrado de la diferencia.
Geométricamente, el área del cuadrado de una diferencia es representada por un cuadrado, ya que todo cuadrado es un rectángulo.
Ejemplo # 1: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.
En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ejemplo # 2: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.

En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ambas soluciones tienen algo en común:
- Su primer término es el cuadrado de el primer término de la diferencia,
- El término del medio es el doble del producto de los dos términos que componen la diferencia y
- El último término de la solución es el cuadrado del último término de la diferencia.
Por lo tanto, podemos crear una regla general para todos los cuadrados de una diferencia:
Caso # 3:
: una suma por una diferencia: términos iguales, signos diferentes
Al multiplicar una suma y una diferencia que tienen los mismos términos, pero tienen el signo diferente, habría que visualizar la suma y la diferencia con dos colores diferentes cuando tracemos el rectángulo. En los siguientes ejemplos, las partes que representen a b estarán coloreadas del color que hemos usado, mientras que las áreas que cubra -b serán coloreadas de blanco.
Ejemplo # 1: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Pintemos de blanco toda la fila de -2 para denotar que esos resultados son negativos.
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.
En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ejemplo # 2: Encontrar el producto:
Solución: Esto se visualiza mejor en el siguiente rectángulo:
Pintemos de blanco toda la fila de -3 para denotar que esos resultados son negativos.
Ahora encontremos el área de todos los rectángulos internos y sumémoslos.
En este caso, la fórmula para el área asociada es:
Área .
Por lo tanto, podemos concluir que:
.
Ambas soluciones tienen algo en común:
- El primer término de la solución es el cuadrado de el primer término, sea de la suma o la diferencia,
- El término del medio es cero. La razón: se formaron dos áreas iguales: una positiva y otra negativa. Al ser del mismo tamaño, pero diferente color, se eliminan entre sí
- El último término de la solución es el opuesto del cuadrado del último término de la suma o la diferencia.
Por lo tanto, queda una diferencia de dos cuadrados. Podemos crear una regla general para todas las diferencias de dos cuadrados:

Multiplicación de Polinomios
Debe ser claro que este método se puede usar con la multiplicación de dos polinomios cualesquiera. Por ejemplo, (ax + b)(cx2 + dx + e) se puede visualizar en la siguiente manera:
Agrupando términos nos da que
(ax + b)(cx2 + dx + e) =acx3 + (bc+ad)x2 + (bd+ae)x + be.

Resumen
Ahora que usted ha terminado esta lección, usted debe poder:
- Multiplicar dos binomios y reconocer como ese producto se puede visualizar usando el área de un rectángulo.
- Reconocer los casos especiales:
- (ax + b)2
- (ax - b)2
- (ax + b)(ax - b)
- Multiplicar dos polinomios y reconocer como ese producto se puede visualizar usando el área de un rectángulo.
|