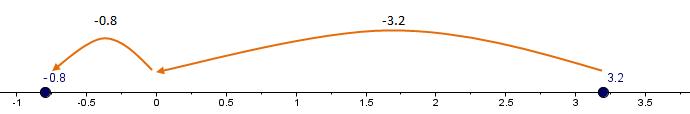Al concluir esta lección, deberás ser capaz de:
-
Leer decimales como suma de fracciones
- Ordenar decimales de menor a mayor
- Sumar y restar decimales como fracciones.
- Identificar donde se ubican decimales en la recta real.
- Sumar y restar decimales usando la recta real.
Representación de Números Decimales como Fracciones
En la notación decimal que utilizamos para los números, 4623 expande a 4 mil, 6 ciento, 2 diez y 3 unidades. Desde izquierda hacia la derecha, el primer dígito representa miles (1000's), el próximo dígito representa cientos (100's) y con cada posición que se mueve a la derecha, el valor que representa la posición del dígito disminuye por un factor de un decimo.
En los números con un punto decimal el valor de cada dígito disminuye por un factor de 1/10 para cada posición que se mueve a la derecha pero se permiten fracciones. Se utiliza el punto decimal para representar valores que no son enteros.
En un número decimal la parte entera está a la izquierda del punto decimal y la parte fraccional está a la derecha del punto decimal. Sigue la regla de leer desde la izquierda a la derecha, cada posición que se mueve a la derecha reduce el valor del dígito por un factor de . Por ejemplo,

La posición del punto decimal define el tamaño relativo de un número. Así 10.5 es diez veces más grande que 1.05. El primero representa 10 unidades enteros y 5 décimos de unidad mientras el segundo representa 1 unidad entero y 5 centésimos de unidad. Utiliza la aplicación siguiente para mostrar que entiendes el tamaño relativo de números decimales.
Representación de Números Decimales en la Recta Real
En la aplicación de abajo, sigues los siguientes pasos:
- Mueve el botón de abajo hasta que muestra b sea igual a 1. El largo de 1 / b se presenta en verde.
- En la fracción a / b, a representa la cantidad de unidades. Así cuando a se mueve desde 1 hasta 5, la posición en la recta real va desde 1 hasta 5. Practiques eso.
- Ahora, mueve el botón de abajo hasta que muestra b sea igual a 10.
- Ahora en la nueva fracción a / b, a representa la cantidad de decimos. Cuando a se mueve desde 1 hasta 10, la posición en la recta real va desde 0.1 (un décimo) hasta 1.0 (10 décimos). Practiques eso
Para mostrar que has entendido la relación entre decimales y la recta real, sigue los siguientes pasos con la aplicacion de abajo:
- Encuentres el lugar donde pertenece el punto asociado con el numero entero indicado en la recta real. Cuando las instrucciones indican que apretes zoom, que aprestes el simbolo de + para ver con mas detalle donde pertence el punto.
- Apretes el botón que dice Siguiente Problema hasta que estes comodo(a) encontrando la localización de numeros enteros en la recta real.
- Cuando puedes localizar numeros enteros, usar la flecha al lado de Posiciones para escoger Decimales.
- Sigues el mismo procedimiento para encontrar la localización de numeros decimales en la recta real.
- Apretes el botón que dice Siguiente Problema hasta que estes comodo(a) encontrando la localización de numeros decimales en la recta real.
Applet Cortesia del National Library of Virtual Manipulatives (nlvm.usu.edu).

La aplicación siguiente es un repaso de cómo representar la suma y la resta de números enteros en la recta real.
Los ejemplos siguientes muestra cómo funciona la aplicación:
- Colocar el botón azul en el 2 y el botón rojo en el 5. La aplicación muestra: cuando comienza en el 2 y se mueve 5 unidades hacia la derecha en la recta real, llegamos al 7. En otras palabras muestra que 2 + 5 = 7.
- Colocar el botón azul en el –3 y el botón rojo en el –6. La aplicación muestra: cuando comienza en el –3 y se mueve 6 unidades hacia la izquierda, llegamos al –9. En otras palabras –3 + (–6) = –3 – 6 = –9.
- Colocar el botón azul en el 4 y el botón rojo en el –9. La aplicación muestra: cuando comienza en el 4 y se mueve 9 unidades hacia la izquierda pasamos por el 0 (4 unidades a la izquierda del 4) y llegamos al –5 (5 unidades a la izquierda del 0). En otras palabras 4 + (–9) = 4 – 9 = –5.
- Colocar el botón azul en el –6 y el botón rojo en el 8. La aplicación muestra: cuando comienza en el –6 y se mueve 8 unidades a la derecha pasamos por el 0 (6 unidades a la derecha del –6) y llegamos al 2 (2 unidades a la derecha del 0). En otras palabras –6 + 8 = 2.
Sigues practicando con (i)-5 - 2, (ii) 3 + 6, (iii) 7 - 9, (iv) -1 + 4 y (v) tus propios ejemplos!
La siguiente aplicación presenta el mismo concepto de como sumar y restar números usando la recta real pero con números decimales.
Por favor seguir los siguientes pasos
- Mover el botón baja Restar a la izquierda para que diga sumar, asegurar que Escala = 0.1 y sigues los siguientes pasos:
- Poner el botón rojo en 0.3 y el botón azul en 0.7. Se ve que al comenzar en 0.3 y mover 0.7 unidades a la derecha, terminamos en 1.0. Es decir que 0.3 + 0.7 = 0.3 - -0.7 = 1.0.
- Poner el botón rojo en -0.6 y el botón azul en 0.8. Se ve que al comenzar en -0.6 y mover 0.8 unidades a la derecha que los primeros 0.6 unidades nos lleva de -0.6 a 0 y los próximos 0.2 unidades nos lleva de 0 a 0.2 así terminamos en 0.2. Es decir que -0.6 + 0.8 = -0.6 - -0.8 = 0.2.
- Mover el botón baja Sumar a la derecha para que diga Restar, asegurar que Escala = 0.01 y sigues los siguientes pasos:
- Poner el botón rojo en -0.02 y el botón azul en 0.07. Se ve que al comenzar en -0.02 y mover 0.07 unidades a la izquierda, terminamos en -0.09. Es decir que -0.02 - 0.07 = -0.02 + -0.07 = -0.09.
- Poner el botón rojo en 0.04 y el botón azul en 0.05. Se ve que al comenzar en 0.04 y mover 0.05 unidades a la izquierda que los primeros 0.04 unidades nos lleva de 0.04 a 0 y los próximos 0.01 unidades nos lleva de 0 a -0.01 así terminamos en -0.01. Es decir que 0.04 - 0.05 = 0.04 + -0.05 = -0.01
Sigues practicando con (i)-0.5 - 0.2, (ii) 0.04 + 0.06, (iii) 0.5 - 0.9, (iv) -0.02 + 0.04 y (v) tus propios ejemplos!
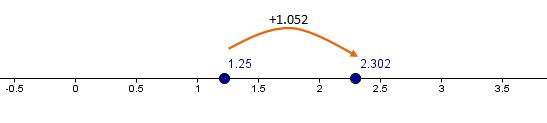
Con esta práctica, debes poder seguir el procedimiento algebraico y geométrico en los siguientes ejemplos:
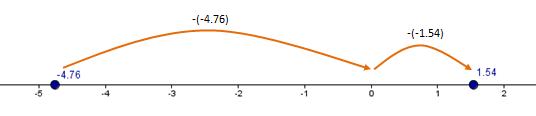
Ejemplo 1:

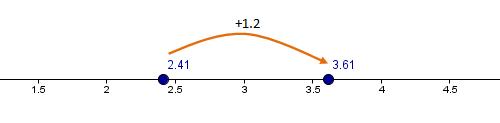
Ejemplo 2:
Ejemplo 3:
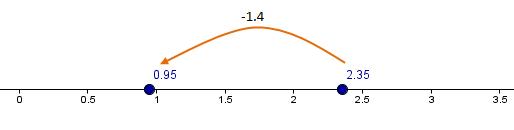
Ejemplo 4:
Ejemplo 5:
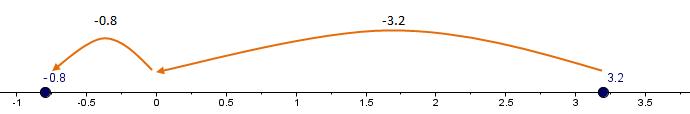
Ejemplo 6:
Ejemplo 7:
Ejemplo 8:
Ejemplo 9:
Ejemplo 10:

Oprime el botón de abajo para practicar restando y sumando decimales con la recta real.

Oprime los botones de abajo para practicar restando y sumando decimales sin la recta real.


Ahora que has completado esta lección, eres capaz de:
-
Leer decimales como suma de fracciones
- Ordenar decimales de menor a mayor
- Sumar y restar decimales como fracciones.
- Identificar donde se ubican decimales en la recta real.
- Sumar y restar decimales usando la recta real.
|