Funciones Cuadráticas y sus RaícesObjetivosAl concluir esta lección, deberás ser capaz de:
IntroducciónMuchas aplicaciones de la vida real pueden ser modeladas con funciones cuadráticas. En esta lección vamos a estudiar las funciones cuadráticas y vamos a aprender cómo obtener las raíces de la función. Veamos la siguiente aplicación que nos permite visualizar funciones cuadráticas.
Aplicación Cortesia de www.educaplus.orgMueve los puntos para que cambien los valores de los parámetros de la ecuación. Qué características puedes observar de la ecuación al lado izquierdo?. Qué puedes decir a cerca de la gráfica? En este tutorial haremos una introducción a las funciones cuadráticas y cómo obtener las raíces de estas funciones. Definición
La representación anterior es conocida como la forma general de una función cuadrática. Una función cuadrática puede ser vista como una máquina:
donde los valores de a, b y c son valores conocidos por la máquina Así por ejemplo, si tenemos la siguiente máquina:
y el valor de x es 5, entonces la máquina nos dará el siguiente valor de salida:
Raíces de una Función CuadráticaLa siguiente aplicación nos muestra otra forma de expresar las funciones cuadráticas. Aplicación Cortesia de www.educaplus.orgEn la aplicación anterior al escoger a = 1, y resulta la gráfica de la ecuación cuadrática Selecciona la caja rotulada Intersección con el eje. Nota que y son los valores de x donde f(x) = 0. Estos valores se conocen como las raíces de la función cuadrática. Si realizamos la multiplicación, obtenemos la fórmula de la función correspondiente en su forma general. f(x) = x2 - 3x + 2. Esto nos indica que si tenemos la fórmula y la factorizamos obtenemos las raíces de una función cuadrática. En esta sección utilizaremos lo aprendido en la lección de factorización. Función Cuadrática con dos Raíces RealesEjemplo: Encontrar las raíces de la función Solución:Como las raíces son los valores donde la función es 0, buscamos resolver la ecuación f(x)=0 Factorizando la expresión obtenemos Como el producto anterior es cero, entonces:
Las raíces de la función son x=5 y x=-2 Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
Función Cuadrática con una Raíz RealEjemplo: Encontrar las raíces de la función Solución:Como las raíces son los valores donde la función es 0, buscamos resolver la ecuación f(x)=0 Factorizando la expresión obtenemos
Como f(x)=0, entonces:
Las función tiene una raíz y es x=1 Como vemos en la siguiente figura, la gráfica de la función toca el eje x sin cruzarlo, por lo que sólo tiene una raíz:
Función Cuadrática sin Raíces RealesEjemplo: Encontrar las raíces de la función Solución:Como las raíces son los valores donde la función es 0, buscamos resolver la ecuación f(x)=0 Cuando vemos que no es muy facil la factorización podemos recurrir a la fórmula cuadrática. Estudiamos la fórmula cuadrática en la leccion ecuaciones cuadraticas. Las raíces de la función son y Cuando la gráfica no intercepta el eje x, las raíces de la función cuadrática son imaginarias, como vemos en la gráfica correspondiente:
Haga clic en el siguiente enlace para practicar la forma de encontrar la raices de una función cuadrática: Relación entre las Raíces y los Factores de una Función CuadráticaComo vimos en los ejemplos previos, existe una relación entre los factores de la función cuadrática y sus raíces.
Como consecuencia, podemos afirmar lo siguiente:
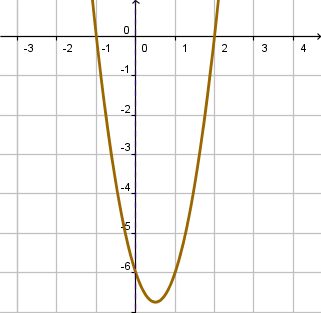
Ejemplo 1: Hallar la función cuadrática cuyas raíces son 2 y -1 y cuyo intercepto es -6. Solución: Por la relación que existe entre las raíces y los factores de la función cuadrática, esta tendrá la forma:
Ademas como el intercepto es -6, significa f(0)=-6 Reemplazando x=0 en la fórmula anterior:
De donde:
y entonces:
Finalmente, la función que buscamos es:
Esta es la gráfica de la función. Puedes verificar que la función tiene las raíces 2 y -1 y su intercepto es -6.
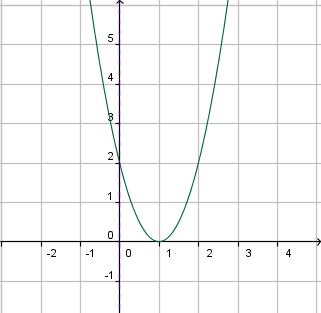
Ejemplo 2: Hallar la función cuadrática cuya única raíz es 1 y cuyo intercepto con el eje de y es 2. Solución: Por la relación que existe entre las raíces y los factores de la función cuadrática, esta tendrá la forma:
Ademas como el intercepto es 2, significa f(0)=2 Reemplazando x=0 en la fórmula anterior:
De donde:
Finalmente, la función que buscamos es:
Esta es la gráfica de la función. Puedes verificar que su raíz es 1 y su intercepto es 2.
Ejemplo 3: Hallar la función cuadrática cuyas raíces imaginarias son i y -i y cuyo intercepto con el eje de y es 2. Solución: Por la relación que existe entre las raíces y los factores de la función cuadrática, esta tendrá la forma:
Ademas como el intercepto es 2, significa f(0)=2 Reemplazando x=0 en la fórmula anterior:
Finalmente, la función que buscamos es:
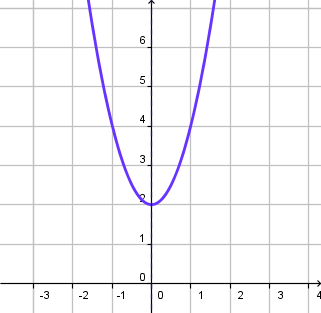
Esta es la gráfica de la función. Puedes verificar que no tiene raíces reales y su intercepto es 2.
Práctica En la siguiente aplicación, determine las raices de la función que se le indica ResumenAhora que has completado esta lección, eres capaz de:
|