Funciones Polinómicas y sus RaícesObjetivosAl concluir esta lección, deberás ser capaz de:
IntroducciónHemos estudiado las funciones lineales y las funciones cuadráticas. Estas funciones son casos especiales de funciones polinómicas. Las funciones polinómicas nos permiten modelar muchas aplicaciones de la vida real. En este tutorial haremos una introducción a las funciones polinómicas y cómo obtener las raíces de estas funciones. DefiniciónEn la lección de Expresiones Algebraicas y Polinomios aprendimos a identificar polinomios y sus componentes. Ahora vamos a estudiar funciones definidas por polinomios.
La representación anterior es conocida como la forma general de una función polinómica. Raíces de una Función Polinómica
Lo anterior significa que, para encontrar las raíces de la función polinómica f, resolvemos la ecuación f(x)=0. Recordemos que en la lección resolución de ecuaciones, aprendimos que si A×B=0 entonces A=0 o B=0. Por lo tanto, necesitamos factorizar f(x), e igualar cada factor a cero. En la lección Factorización por agrupación aprendimos a factorizar polinomios. Ejemplo 1: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos: Recordemos que si A×B=0 entonces A=0 o B=0. Por lo que:
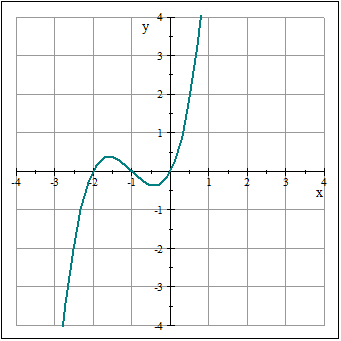
Las raíces de la función son x=0, x=-1 y x=-2 Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
Ejemplo 2: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos: Recordemos que si A×B=0 entonces A=0 o B=0. Por lo que:
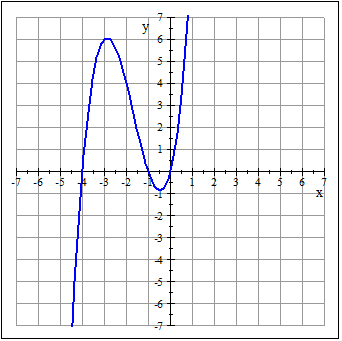
Las raíces de la función son x=0, x=-1 y x=-4 Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
Raíces dobles y triples
Ejemplo 1: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos: Por lo que:
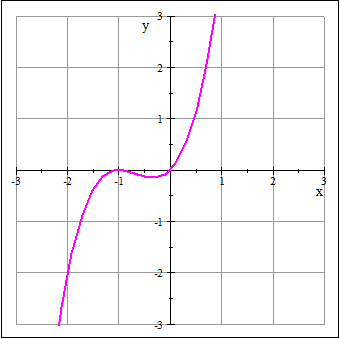
Las raíces de la función son x=0 y x=-1 Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
Ejemplo 2: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos: Por lo que:
La raíz de la función es x=-1 Puedes visualizar estas raíces observando la gráfica de esta función, que es la siguiente:
Vemos que el factor (x+1) aparece tres veces. Este genera una raíz triple x=-1. Vemos en la gráfica que la curva toca el eje x y lo cruza. En general,
Haga clic en el siguiente enlace para practicar la forma de hallar las raices de un polinomio: Raíces imaginarias y complejasEjemplo 1: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos: Recordemos que siempre es posible utilizar la fórmula cuadrática cuando es dificil encontrar los factores. De la expresión anterior:
Las raíces de la función son x=0, x=i y x=-i La gráfica de esta función es la siguiente:
En la gráfica podemos visualizar la raíz real x=0. Este polinomio tiene una raíz real y dos raíces imaginarias, en total 3 raíces complejas. Ejemplo 2: Encontrar las raíces de la función Solución:Buscamos resolver la ecuación f(x)=0. Factorizando la expresión obtenemos:
Recordemos que siempre es posible utilizar la fórmula cuadrática cuando es dificil encontrar los factores. De la expresión anterior:
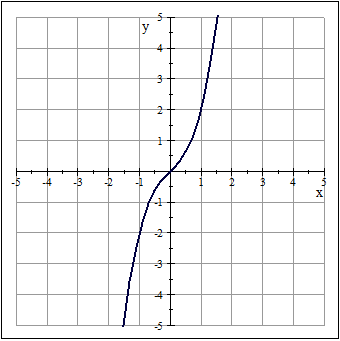
Las raíces de la función son x=0, x=2+i y x=2-i La gráfica de esta función es la siguiente:
En la gráfica podemos visualizar la raíz real x=0. Es importante notar que el punto de inflexión señalado por la flecha, no toca el eje x. Esto es un indicativo de la existencia de raíces con parte imaginaria. Este polinomio tiene 3 raíces complejas.
Por ejemplo: Las raíces complejas de la función son los pares conjugados x=i y x=-i Las raíces complejas de la función son los pares conjugados x=2+i y x=2-i Teorema Fundamental del Algebra
Ejemplo 1: Encontrar todos los factores complejos de la función Solución:Factorizando la expresión obtenemos:
Recordemos que siempre es posible utilizar la fórmula cuadrática cuando es dificil encontrar los factores. De la expresión anterior:
Las raíces de la función son x=0, x=2+i y x=2-i Ahora, podemos utilizar las raíces para escribir la función en su forma factorizada: Ejemplo 2: Encontrar todos los factores complejos de la función Solución:Factorizando la expresión obtenemos:
Solución:
No siempre es fácil convertir un polinomio a su forma factorizada pero sabemos que siempre es posible escribirlo en esa forma. ResumenAhora que has completado esta lección, eres capaz de:
|
 0
0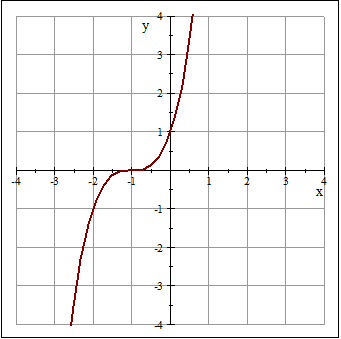

 0
0