Objetivos:
- Entender los conceptos básicos de la geometría plana.
- Introducir los elementos básicos de la geometría.
- Reconocer figuras geométricas planas.
Introducción
Introducción
El estudio de la geometría debe incluir experiencias y actividades que les permita a los estudiantes entender el significado de la geometría en sus vidas del diario vivir. Es importante que los estudiantes desarrollen habilidades inductivas usando manipulativos o programado de computadoras. Además es importante el aprendizaje en grupo que les permita discutir la solución de los problemas y las conexiones de la geometría con las otras disciplinas como álgebra y cálculo.
La geometría es muy importante debido a que permite enseñar y aprender el arte de razonar, porque es abstracta, pero fácil de visualizar y tiene muchas aplicaciones concretas como por ejemplo, calcular el área de un lote a ser cercado, determinar el volumen de un lata que contiene refresco, construir puentes bien estructurados, estaciones experimentales en el espacio, grandes coliseos deportivos, etc. A continuación se muestra la iglesia de Santa Sofía construída en los años 300, pertenece a la arquitectura Bizantina y fue diseñada usando figuras geométricas, como semiesferas, rectángulos.
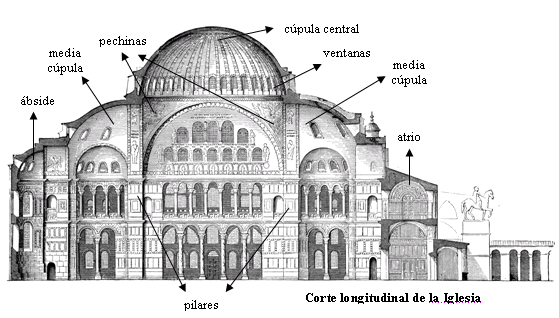
Iglesia de Santa Sofía
La geometría elemental se divide en dos partes, geometría plana (estudia la figuras planas, que tienen únicamente dos dimensiones: largo y ancho) y geometría del espacio (estudia las propiedades de los cuerpos geométricos provistos de largo, ancho y altura o profundidad).
Geometría plana
La geometría plana estudia las figuras planas, que tienen únicamente dos dimensiones: largo y ancho.
Para comprender la geometría plana de manera mas clara, es indispensable, comenzar por la definición de
conceptos elementales hasta llegar a nociones más complejas.
Conceptos básicos
Para el estudio de la geometría, es indispensable conocer el concepto intuitivo de punto, recta y plano. Estos son términos no definidos que proveen el inicio de la geometría.
Punto es el objeto fundamental en geometría, el punto representa solo posición y no tiene dimensión, es decir, largo cero, ancho cero y altura cero. Se representan por letras mayúsculas.
Ejemplo:
Tres puntos
Recta tiene solo longitud, no tiene ancho ni altura ni grosor. Es un conjunto infinito de puntos que se extienden en una dimensión en ambas direcciones. Una recta se puede representar por:
Semirrecta la definimos como la porción de una recta que tiene principio pero no tiene fin.
segmento de recta es una porción de la recta con principio y con fin, es decir sabemos donde empieza y donde termina por ende lo podemos medir.
Plano tiene ancho y largo, sin altura ni grosor. Un plano es una superficie en dos dimensiones, se puede pensar como un conjunto de puntos infinitos en dos dimensiones.

En la siguiente aplicación, mueve y manipula los elementos básicos en el plano. Indica cuales de los elementos presentes son puntos, cuales son rectas, cuales son semirrectas y cuales son segmentos.
¿Se pueden medir todos los elementos que ves en la imagen? Razona la respuesta.
¿Dirías que el punto "D" pertenece a la recta "a" ?
Polígonos
Un polígono es una figura plana cerrada que está formada por tres o más segmentos de recta que se unen en sus puntos extremos. Los segmentos de recta que forman un polígono solo se intersectan en sus puntos extremos. Los polígonos se nombran de acuerdo al número de lados que están formados.
|
Triángulo: polígono de 3 lados Cuádrilatero: polígono de 4 lados Pentagono: polígono de 5 lados Hexágono: polígono de 6 lados Heptágono: polígono de 7 lados |
Octágono: polígono de 8 lados Nonágono: polígono de 9 lados Decágono: polígono de 10 lados Dodecágono: polígono de 12 lados n - ágono: polígono de n lados |
Ejemplos de polígonos:
|
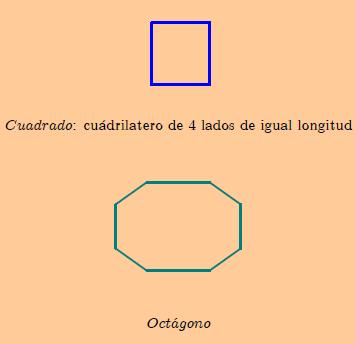
|
En la siguiente aplicación, se muestran las graficas de los polígonos regulares según la cantidad de lados.
Para detener la animación pulsa el botón del lado inferior izquierdo. A lado derecho puedes mover el punto
negro para cambiar el numero de lados del polígono. Observa como cambia la figura y el nombre de cada una de ellas.
Las partes de un polígono son:
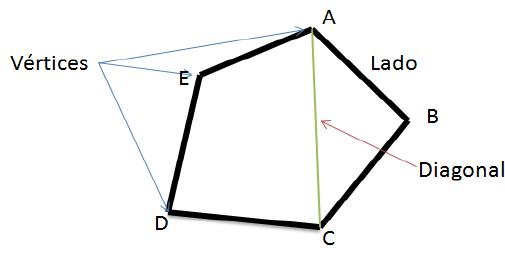
Vértices: puntos finales de los segmentos que forma el polígono, en la figura: A, B, C, D, E.
Lados: segmentos de recta que unen dos vértices consecutivos del polígono, en la figura los lados son: AB,
Lados consecutivos: cualquier par de lados que comparten un vértice, en la figura: AB y BC, BC y CD,
Diagonal: un segmento de recta que une dos vértices no consecutivos, en la figura: AC.
Apotema: de un polígono regular es la menor distancia entre el centro y cualquiera de sus lados. Es un segmento cuyos extremos son el centro de un polígono regular y el punto medio de uno cualquiera de sus lados, y es siempre perpendicular a dicho lado.
Círculos
El círculo es una figura plana que consiste de todos los puntos que están sobre una curva cerrada y de los puntos interiores de ella, en la cual cada punto sobre la curva tiene la misma distancia al centro del círculo.
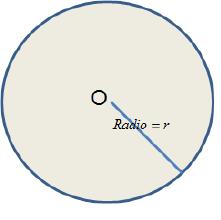
El radio de un círculo es la distancia entre el centro y cualquier punto de la curva y tiene longitud r.
El diámetro de un círculo es la distancia entre dos puntos cualesquiera de la curva cerrada y que pasa por el centro y tiene longitud d = 2r y divide a un círculo en dos partes iguales.
La Circunferencia es la línea curva cerrada y plana cuyos puntos están a la misma distancia (radio) de un punto (centro). El centro no es parte de la circunferencia.
El área de un círculo, es la medida de la superficie limitada por la circunferencia del círculo dado.
En la siguiente aplicación mueve los deslizadores y luego:
- Compara las superficies del polígono inscrito en la circunferencia y la del círculo delimitado por la misma.
- Aumenta el número de lados y cambia la longitud del radio ¿Qué harías para que la superficie del polígono fuese lo más parecida posible a la del círculo?
- Activa las casillas "Datos del polígono" y "Radio". Repite las actividades uno y dos. Comprueba que la respuesta que has dado en la actividad dos es la correcta.
- Activa las casillas "Área del polígono" y "Área del círculo". Comprueba si la respuesta dada en la actividad dos es acorde con los datos de las áreas.
Resumen
Ahora que has terminado la lección, eres capaz de:
- Entender los conceptos básicos de la geometría plana.
- Reconocer los elementos básicos de la geometría.
- Reconocer figuras geométricas planas.
File applications developed with GeoGebra