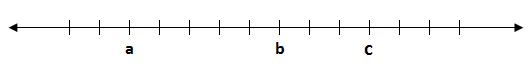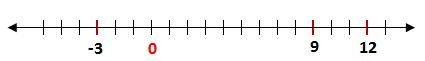Introducción a Desigualdades
Al concluir esta lección, deberás ser capaz de:
- Reconocer cuando una desigualdad es cierta o falsa
- Aplicar la propiedad transitiva de desigualdades
- Usar propiedades de desigualdades para solucionar inecuaciones
Introducción:
Es la última semana del semestre, Tato necesita obtener un promedio mayor que 65 para aprobar el curso de química. El peso relativo de cada prueba del curso y las notas obtenidas por Tato se desglosan en la siguiente tabla.
| Peso Relativo | Nota de Tato |
|---|
| Prueba 1 | 15% | 68 |
| Prueba 2 | 30% | 54 |
| Prueba 3 | 35% | 66 |
| Examen Final | 25% | x |
Si se calcula el promedio siguiendo las puntuaciones y sus pesos relativos tenemos:
La nota x, en el examen final, que necesita obtener Tato para pasar el curso, está en el conjunto de valores que satisfacen:
Ahora le toca a Tato convertir esta relación, en una expresion como x > (algún valor) para que sepa con cuales notas en el examen final se asegura de pasar la clase. En esta y las próximas lecciones asociadas con inecuaciones, aprenderás a resolver inecuaciones como la anterior. Verás que la presencia del signo de desigualdad en el enunciado tiene consecuencias tanto sobre el procedimiento de encontrar la solución como con la interpretación de la solución.
!Éxito!
Definiciones:
Si
a,
b
pertenecen a los
Números Reales
,
entonces escribimos
si
a
es menor que
b.
Otro manera de decir eso es que a se localiza a la izquierda de b en la recta real.
|
Si
a,
b
pertenecen a los
Números Reales
,
entonces escribimos
si
a
es mayor que
b.
Otro manera de decir eso es que a se localiza a la derecha de b en la recta real.
|
Una consecuencia natural de estas definiciones es que
|
Los símbolos
≤
(“ menor o igual a ”) y
≥
(“ mayor o igual a ”) se definen de la siguiente manera:
a ≤ b
si y sólo si a < b ó a = b
a ≥ b
si y sólo si a > b ó a = b
|
|
| Las relaciones
a
< b,
a > b,
a ≤
b y a ≥b se llaman desigualdades |
Las representaciones del “conjunto solución ” de desigualdades en una variable (inecuaciones) se discutirán en la próxima lección acerca de intervalos.
En esta lección discutiremos definiciones, propiedades y el uso de propiedades para resolver inecuaciones.
|

Propiedades de las Desigualdades.
Sean
a,
b,
c
números reales
Propiedad # 2: Suma y Resta
Si a < b y c es un número real entonces,
a + c < b + c y a
– c < b – c
Sea c=2
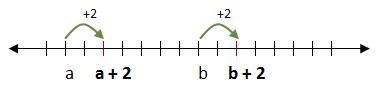
Sea c=-3

|
Ilustraciones:
-3 <
9 entonces -3 +
6 < 9 + 6
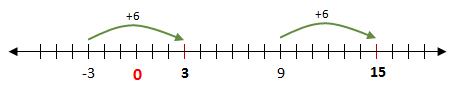
Ya que -3 esta a la izquierda de 9, entonces si sumamos 6 a ambos. Entonces -3+6 también está a la izquierda de 9+6.
-3 < 9
entonces -3 – 6 < 9 – 6
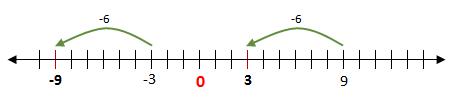
Ya que -3 está a la izquierda de 9, entonces si restamos 6 a ambos. Entonces -3-6 tambeinén está a la izquierda de 9+6.
|
|
Propiedad # 3: Multiplicación
Si a < b y c es un
número real positivo entonces
ca < cb
Ilustración:
-3
<4 entonces
2(-3) < 2(4)
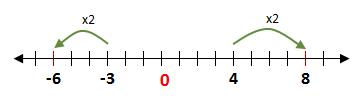
|
Si a < b y c es un número real negativo entonces,
ca >
cb
Ilustración:
-2 es un número negativo
-3 <4 entonces
(-2)(-3) > (-2)(4)
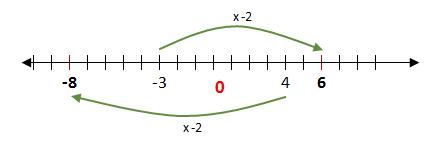
|
|
Propiedad # 4: División
Si a < b y c es un
número real positivo entonces
Ilustración:
-3
< 9 entonces
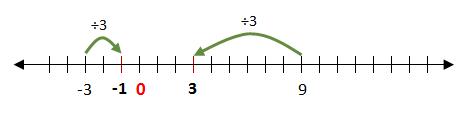
|
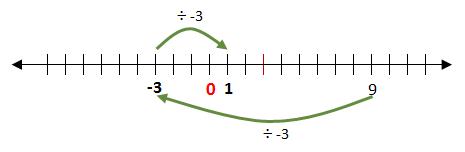
Si a < b y c es un número real negativo entonces,
Ilustración:
-3 es un número negativo
-3 <
9 entonces
|
|

Usando Propiedades para Simplificar Inecuaciones Sencillas
Objetivo: Dada una desigualdad que contiene la incógnita
x ,
nuestro objetivo es usar las propiedades de desigualdades para aislar
la variable x a un lado del signo de desigualdad. Al otro lado del signo de desigualdad tendremos entonces la solución.
Ejemplos
Ejemplo 1: Simplificar
5 +
x
< 9 .
Solución:
Nuestro objetivo es convertir
5 +
x
< 9
en
x
< ...
Para hacer eso utilizamos los siguientes pasos
|
Paso 1.
Identificar la operación inversa necesaria para aislar x.
En este caso: restar 5
|
|
Paso 2.
Utilice la propiedad # 2: reste
5
a ambos lados de la desigualdad.
5 + x
- 5
<+ 9
- 5
Asi la inecuación simplificada es
x < 4
|
Ejemplo 2: Simplificar
Solución: Nuestro objetivo es convertir
o escrito de otra manera:
en
así que utilizaremos los siguientes pasos:
|
Paso 1.
Identificar la operación inversa necesaria para aislar el término que contiene la variable x. En este caso: restar 3
|
|
Paso 2.
Utilice la propiedad # 2: reste 3
a ambos lados de la desigualdad
Asi la inecuación que resulta es:
|
|
Paso 3.
Utilice la propiedad # 3: multiplique por 2 (operación inversa de la división)
ambos lados de la desigualdad
Asi la inecuación simplificada es
|
Ejemplo 3: Simplificar
Solución: Nuestro objetivo es convertir
en
así que utilizaremos los siguientes pasos:
|
Paso 1.
Identificar la operación inversa necesaria para aislar el término que contiene la variable x. En este caso: restar 1
|
|
Paso 2.
Utilice la propiedad # 2: reste 1
a ambos lados de la desigualdad
Asi la inecuación que resulta es:
|
|
Paso 3.
Utilice la propiedad # 4: divida por -3
ambos lados de la desigualdad
Es importante recordar que división y multiplicación con
un número negativo cambia la dirección de la desigualdad
así la inecuación simplificada es
|

Ya que has concluido esta lección, debes ser capaz de:
- Reconocer cuando una desigualdad es cierta o falsa
- Aplicar la propiedad transitiva de desigualdades
- Usar propiedades de desigualdades para solucionar inecuaciones
|