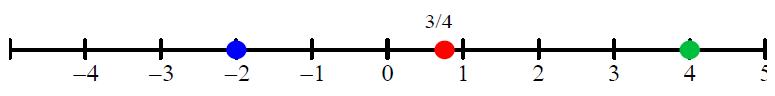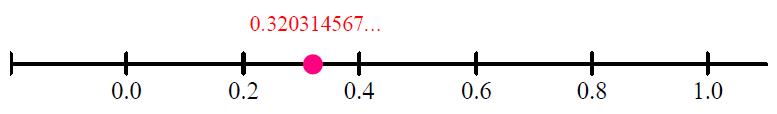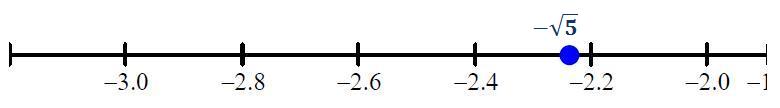Sistemas de numeración1 Objetivos:
2 IntroducciónEl sistema de los números reales ha evolucionado con el tiempo y está relacionado con el significado de la palabra número, y son parte de nuestra vida diaria. Se usa continuamente y de manera inconsciente, en simples cálculos, en las cuentas de la casa, el banco, el presupuesto, la hora, compras, ventas, etc.Luego las operaciones entre números aparecieron como reflejo de las relaciones entre objetos concretos, así por ejemplo se estableció que una suma no depende del orden de los sumandos. A medida que la sociedad iba evolucionando, el hombre se vio ante la necesidad de perfeccionar los nombres y símbolos de los números y posteriormente la introducción de signos y designación literal de las incógnitas o variables. Por ejemplo, los babilonios tenían un sistema de escritura de los números que era parcialmente decimal y parcialmente sexagesimal. En sus últimas escrituras cuneiformes ya apareció el cero, aunque fueron los indios los que verdaderamente lo introdujeron, al que llamaron "vacío", y les permitió elaborar un sistema de escritura análogo al que se usa en la actualidad. Los antiguos griegos y posteriormente los rusos, hicieron uso de letras para designar números siendo, no obstante, los árabes los que trajeron a Europa de la India nuestros símbolos actuales y el método de formación de números. En el estudio de los números reales se considera el sistema decimal cuyos símbolos llamadas cifras son: 3 Diferentes tipos de númerosSe puede decir que un número es una entidad abstracta que representa una cantidad, a continuación se definen los diferentes tipos de números:3.1 Números naturalesSon los números usados por los hombres para contar objetos. Se representan por la letra y los elementos de este conjunto son:3.2 Números enterosEs el conjunto de números que contiene tanto los valores enteros positivos (o naturales), el cero y los negativos (enteros negativos). Se caracterizan porque siempre van precedidos de un signo que los identifica: '+' para los positivos o '-' para los negativos. Se representan por la letra (en alemán, Zahl, significa número) y los elementos de este conjunto son:enteros negativos enteros positivos En otras palabaras, el conjunto de los números enteros se puede representar como: 3.3 Números racionalesEs el conjunto de los números que se pueden expresar como una fracción de dos números enteros, donde el denominador debe ser diferente de cero. Se representa por la letra y sus elementos son de la forma:Además, todonúmero racional tiene michas representaciones, por ejemplo: es equivalente a ó . Por otro lado, cada número racional tiene una representación decimal que se obtiene dividiendo el numerador entre el denominador y son: 3.3.1 Decimal finitoAquellos que tienen división exacta, por ejemlo:3.3.2 Decimal infinitoAquellos cuya división es periódica infinita, por ejemplo:3.4 Números irracionalesLos números irracionales son aquellos que no pueden expresarse como la fracción de dos números entreros y se denotan por la letra . Son números decimales que no tienen ningún patrón, es decir, su expresión decimal es ilimitada y no periódica. Por ejemplos:
3.5 Subconjuntos de los Números RealesEl conjunto de los números reales es el conjunto de todos los números racionales y todos los números irracionales, se denotan por la letra yR={x|x es racional o x es irracional} La siguiente gráfica representa la clasificación de los números:En términos de conjuntos se tienen las siguientes relaciones: 3.6 Ejemplos

4 La recta realSi en una recta se identifica un origen, el cero (0) y se marca la longitud unidad, a cada punto le corresponde un número racional o un número irracional. Es decir, a cada punto de la recta le corresponde un número real y a cada número real le corresponde un único punto sobre la recta . Por esta razón a la recta numérica se le llama la recta real.
4.1 Representación de números sobre la recta realTodo número real puede representarse en la recta real, dependiendo del tipo de número.4.1.1 Representación de naturales, enteros o decimales finitosSe puede determinar con precisión el punto que le corresponde sobre la recta real. Por ejemplo, represente en la recta real los siguientes números:
4.1.2 Representación de decimales infinitos o periódicosPueden expresarse en forma de fracción y representar la fracción (se divide cada unidad en tantas partes como tenga en denominador y se toman tantas como tenga el numerador) o se representa directamente el número decimal. Por ejemplo:
4.1.3 Representación de números irracionalesUn número irracional se representa en la recta real en forma aproximada, ya sea en su forma decimal, o a través de otra representación. Por ejemplo, represente en la recta real los números: y

5.1 Axiomas de la igualdad5.2 Axiomas de la adición
Ejemplos
5.3 Axiomas de la multiplicación
Ejemplos
5.4 Otras Axiomas
6 ResumenAhora que has concluido esta lección, debes ser capaz de:
|